Bài 9.49 trang 62 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.49, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho tam giác ABC vuông tại A, có diện là (24c{m^2}) và nội tiếp đường tròn có bán kính 5cm. Tính bán kính đường tròn nội tiếp tam giác ABC.
Đề bài
Cho tam giác ABC vuông tại A, có diện là \(24c{m^2}\) và nội tiếp đường tròn có bán kính 5cm. Tính bán kính đường tròn nội tiếp tam giác ABC.
Phương pháp giải - Xem chi tiết
+ Tính BC, áp dụng định lí Pythagore vào tam giác ABC vuông tại A tính được \(A{C^2} + A{B^2}\).
+ Tính được \(AB.AC\).
+ Vì \({\left( {AB + AC} \right)^2} = A{B^2} + 2AB.AC + A{C^2}\) nên tính được \(AB + AC\).
+ Gọi I là tâm đường tròn nội tiếp và r là bán kính của đường tròn nội tiếp tam giác ABC.
+ Ta có:
\(S = {S_{AIB}} + {S_{AIC}} + {S_{BIC}} = \frac{1}{2}r\left( {AB + BC + CA} \right)\), từ đó tính được r.
Lời giải chi tiết
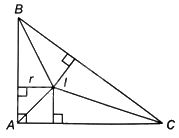
Vì bán kính đường tròn ngoại tiếp tam giác vuông bằng một nửa cạnh huyền nên \(BC = 2.5 = 10\left( {cm} \right)\).
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A ta có: \(A{C^2} + A{B^2} = B{C^2} = 100\).
Vì tam giác ABC có diện là \(24c{m^2}\) nên:
\(\frac{1}{2}AB.AC = 24\) hay \(AB.AC = 48\).
Ta có:
\({\left( {AB + AC} \right)^2} = A{B^2} + 2AB.AC + A{C^2} = 196\),
suy ra \(AB + AC = 14cm\).
Gọi I là tâm đường tròn nội tiếp và r là bán kính của đường tròn nội tiếp tam giác ABC.
Khi đó, r cũng là chiều cao hạ từ đỉnh I xuống các cạnh BC, CA, AB của các tam giác BIC, CIA, ABI.
Ta có: \(S = {S_{AIB}} + {S_{AIC}} + {S_{BIC}} = \frac{1}{2}r\left( {AB + BC + CA} \right)\), suy ra:
\(r = \frac{{2S}}{{AB + BC + AC}} = \frac{{48}}{{10 + 14}} = 2\left( {cm} \right).\)
Bài 9.49 trang 62 sách bài tập Toán 9 - Kết nối tri thức tập 2 yêu cầu chúng ta xét hàm số f(x) = x2 - 4x + 3 và thực hiện các yêu cầu sau:
Hàm số f(x) = x2 - 4x + 3 có dạng f(x) = ax2 + bx + c. Do đó, ta có:
Hoành độ đỉnh của parabol là x0 = -b / (2a) = -(-4) / (2 * 1) = 2.
Tung độ đỉnh của parabol là y0 = f(x0) = f(2) = 22 - 4 * 2 + 3 = 4 - 8 + 3 = -1.
Vậy, đỉnh của parabol là (2; -1).
Để vẽ đồ thị hàm số, ta cần xác định một số điểm thuộc đồ thị. Ngoài đỉnh (2; -1), ta có thể tính thêm một vài điểm khác:
Vẽ parabol đi qua các điểm này, với đỉnh là (2; -1).
Để tìm các điểm mà tại đó hàm số có giá trị bằng 0, ta giải phương trình f(x) = 0:
x2 - 4x + 3 = 0
Phương trình này có hai nghiệm là x1 = 1 và x2 = 3.
Vậy, các điểm mà tại đó hàm số có giá trị bằng 0 là (1; 0) và (3; 0).
Để tìm các giá trị của x sao cho f(x) > 0, ta xét dấu của tam thức bậc hai x2 - 4x + 3.
Vì a = 1 > 0, parabol có hướng mở lên. Hàm số f(x) > 0 khi x nằm ngoài khoảng giữa hai nghiệm của phương trình f(x) = 0.
Vậy, f(x) > 0 khi x < 1 hoặc x > 3.
Thông qua việc giải bài 9.49 trang 62 sách bài tập Toán 9 - Kết nối tri thức tập 2, chúng ta đã củng cố kiến thức về hàm số bậc hai, bao gồm cách xác định hệ số, tính đỉnh, vẽ đồ thị, tìm nghiệm và xét dấu của hàm số. Việc nắm vững những kiến thức này là rất quan trọng để giải quyết các bài toán liên quan đến hàm số bậc hai trong chương trình Toán 9.
Để luyện tập thêm, bạn có thể thử giải các bài tập tương tự trong sách bài tập Toán 9 - Kết nối tri thức tập 2, hoặc tìm kiếm các bài tập trực tuyến trên giaitoan.edu.vn.