Bài 6.33 trang 20 sách bài tập toán 9 Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học toán 9. Bài tập này yêu cầu học sinh vận dụng kiến thức về hệ phương trình bậc nhất hai ẩn để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6.33 trang 20 sách bài tập toán 9 - Kết nối tri thức tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hai hàm số: (y = - frac{3}{2}{x^2}) và (y = {x^2}). a) Vẽ đồ thị của hai hàm số này trên cùng một mặt phẳng tọa độ. b) Tìm điểm A nằm trên đồ thị của hàm số (y = - frac{3}{2}{x^2}) và điểm B nằm trên đồ thị của hàm số (y = {x^2}), biết rằng chúng đều có hoành độ (x = frac{3}{2}). c) Gọi A’, B’ lần lượt là các điểm đối xứng của A, B qua trục tung Oy. Tìm tọa độ của A’, B’ và chứng minh hai điểm này tương ứng nằm trên hai đồ thị của hàm số đi qua A, B.
Đề bài
Cho hai hàm số: \(y = - \frac{3}{2}{x^2}\) và \(y = {x^2}\).
a) Vẽ đồ thị của hai hàm số này trên cùng một mặt phẳng tọa độ.
b) Tìm điểm A nằm trên đồ thị của hàm số \(y = - \frac{3}{2}{x^2}\) và điểm B nằm trên đồ thị của hàm số \(y = {x^2}\), biết rằng chúng đều có hoành độ \(x = \frac{3}{2}\).
c) Gọi A’, B’ lần lượt là các điểm đối xứng của A, B qua trục tung Oy. Tìm tọa độ của A’, B’ và chứng minh hai điểm này tương ứng nằm trên hai đồ thị của hàm số đi qua A, B.
Phương pháp giải - Xem chi tiết
a) Cách vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\):
+ Lập bảng ghi một số cặp giá trị tương ứng của x và y.
+ Trong mặt phẳng tọa độ Oxy, biểu diễn các cặp điểm (x; y) trong bảng giá trị trên và nối chúng lại để được một đường cong là đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\).
b) + Thay \(x = \frac{3}{2}\) vào \(y = - \frac{3}{2}{x^2}\) ta tìm được y, từ đó tìm được tọa độ điểm A.
+ Thay \(x = \frac{3}{2}\) vào \(y = {x^2}\) ta tìm được y, từ đó tìm được tọa độ điểm B.
c) + Hai điểm \(\left( { - {x_o};{y_o}} \right)\) và \(\left( {{x_o};{y_o}} \right)\) là hai điểm đối xứng với nhau qua trục Oy.
+ Thay tọa độ của A’, B’ vào các hàm số \(y = - \frac{3}{2}{x^2}\) và \(y = {x^2}\), ta thu được các đẳng thức luôn đúng nên hai điểm A’, B’ thuộc các đồ thị hàm số đó.
Lời giải chi tiết
a) + Vẽ đồ thị hàm số \(y = - \frac{3}{2}{x^2}\):
Lập bảng một số giá trị tương ứng giữa x và y.

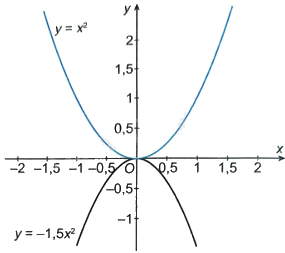
Biểu diễn các điểm \(\left( { - 2; - 6} \right);\left( { - 1; - \frac{3}{2}} \right);\left( {0;0} \right);\left( {1; - \frac{3}{2}} \right),\left( {2; - 6} \right)\) trên mặt phẳng tọa độ Oxy và nối chúng lại ta được đồ thị hàm số \(y = - \frac{3}{2}{x^2}\).
+ Vẽ đồ thị hàm số \(y = {x^2}\):
Lập bảng một số cặp giá trị tương ứng giữa x và y.

Biểu diễn các điểm \(\left( { - 2;4} \right);\left( { - 1;1} \right);\left( {0;0} \right);\left( {1;1} \right);\left( {2;4} \right)\) trên mặt phẳng tọa độ Oxy và nối chúng lại ta được đồ thị hàm số \(y = {x^2}\).
b) Thay \(x = \frac{3}{2}\) vào \(y = - \frac{3}{2}{x^2}\) ta có \(y = - \frac{3}{2}.{\left( {\frac{3}{2}} \right)^2} = \frac{{ - 27}}{8}\) nên \(A\left( {\frac{3}{2};\frac{{ - 27}}{8}} \right)\).
Thay \(x = \frac{3}{2}\) vào \(y = {x^2}\) ta có: \(y = {\left( {\frac{3}{2}} \right)^2} = \frac{9}{4}\) nên \(B\left( {\frac{3}{2};\frac{9}{4}} \right)\).
c) Vì A’ đối xứng với \(A\left( {\frac{3}{2};\frac{{ - 27}}{8}} \right)\) qua trục tung Oy nên \(A'\left( {\frac{{ - 3}}{2};\frac{{ - 27}}{8}} \right)\).
Vì B’ đối xứng với \(B\left( {\frac{3}{2};\frac{9}{4}} \right)\) qua trục tung Oy nên \(B'\left( {\frac{{ - 3}}{2};\frac{9}{4}} \right)\).
Thay \(x = \frac{{ - 3}}{2};y = \frac{{ - 27}}{8}\) vào \(y = - \frac{3}{2}{x^2}\) ta có: \(\frac{{ - 27}}{8} = - \frac{3}{2}.{\left( { - \frac{3}{2}} \right)^2}\) (luôn đúng) nên A’ thuộc đồ thị của hàm số \(y = - \frac{3}{2}{x^2}\).
Thay \(x = \frac{{ - 3}}{2};y = \frac{9}{4}\) vào \(y = {x^2}\) ta có: \(\frac{9}{4} = {\left( {\frac{{ - 3}}{2}} \right)^2}\) (luôn đúng) nên B’ thuộc đồ thị của hàm số \(y = {x^2}\).
Bài 6.33 sách bài tập toán 9 Kết nối tri thức tập 2 yêu cầu giải một bài toán thực tế liên quan đến việc mua vé xem phim. Bài toán này đòi hỏi học sinh phải xây dựng được hệ phương trình bậc nhất hai ẩn từ các thông tin đề bài cung cấp, sau đó giải hệ phương trình để tìm ra giá vé của mỗi loại vé.
Để giải bài toán này, trước tiên chúng ta cần phân tích đề bài một cách cẩn thận để xác định được các yếu tố quan trọng và các mối quan hệ giữa chúng. Sau đó, chúng ta sẽ đặt ẩn số cho các đại lượng chưa biết và biểu diễn các đại lượng khác theo các ẩn số này.
Ví dụ, ta có thể đặt:
Dựa vào các thông tin đề bài cung cấp, ta có thể thiết lập được các phương trình liên quan đến x và y.
Sau khi đã xác định được ẩn số và các mối quan hệ giữa chúng, chúng ta sẽ xây dựng hệ phương trình bậc nhất hai ẩn. Hệ phương trình này sẽ bao gồm các phương trình biểu diễn các điều kiện đề bài.
Ví dụ, nếu đề bài cho biết tổng số tiền mua vé của một nhóm người là bao nhiêu, ta có thể viết phương trình:
ax + by = c
Trong đó a, b, c là các số cụ thể được cho trong đề bài.
Có nhiều phương pháp để giải hệ phương trình bậc nhất hai ẩn, chẳng hạn như phương pháp thế, phương pháp cộng đại số, phương pháp ma trận,… Tùy thuộc vào từng hệ phương trình cụ thể, chúng ta có thể lựa chọn phương pháp phù hợp nhất để giải.
Ví dụ, sử dụng phương pháp thế, ta có thể biểu diễn một ẩn theo ẩn còn lại từ một phương trình, sau đó thay biểu thức này vào phương trình còn lại để tìm ra giá trị của ẩn còn lại. Từ đó, ta có thể tìm ra giá trị của ẩn ban đầu.
Sau khi đã giải được hệ phương trình, chúng ta cần kiểm tra lại kết quả để đảm bảo rằng nó thỏa mãn các điều kiện đề bài. Nếu kết quả không thỏa mãn, ta cần xem xét lại các bước giải và tìm ra lỗi sai.
Giả sử đề bài cho biết:
Một nhóm gồm 5 người lớn và 3 trẻ em đi xem phim. Tổng số tiền mua vé là 150.000 đồng. Biết rằng giá vé của người lớn gấp đôi giá vé của trẻ em. Hãy tính giá vé của mỗi loại vé.
Ta có thể giải bài toán này như sau:
Thay x = 2y vào phương trình 5x + 3y = 150000, ta được:
5(2y) + 3y = 150000
10y + 3y = 150000
13y = 150000
y = 150000 / 13 ≈ 11538.46 đồng
x = 2y ≈ 23076.92 đồng
5(23076.92) + 3(11538.46) ≈ 115384.6 + 34615.38 ≈ 150000 đồng
Vậy giá vé của người lớn là khoảng 23076.92 đồng và giá vé của trẻ em là khoảng 11538.46 đồng.
Khi giải bài tập về hệ phương trình bậc nhất hai ẩn, các em cần lưu ý một số điều sau:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài 6.33 trang 20 sách bài tập toán 9 - Kết nối tri thức tập 2 một cách hiệu quả.