Bài 10.19 trang 71 SBT Toán 9 thuộc chương trình Toán 9 Kết nối tri thức tập 2, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này thường gặp trong các kỳ thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 10.19 trang 71 SBT Toán 9, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
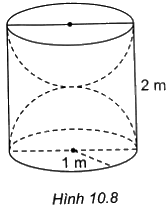
Một khối gỗ hình trụ tròn xoay có bán kính đáy bằng 1m, chiều cao bằng 2m. Người ta khoét từ hai đầu khối gỗ hai nửa hình cầu mà đường tròn đáy của khối gỗ là đường tròn lớn của mỗi nửa khối cầu (H.10.8). Tính tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ ban đầu.
Đề bài
Một khối gỗ hình trụ tròn xoay có bán kính đáy bằng 1m, chiều cao bằng 2m. Người ta khoét từ hai đầu khối gỗ hai nửa hình cầu mà đường tròn đáy của khối gỗ là đường tròn lớn của mỗi nửa khối cầu (H.10.8). Tính tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ ban đầu.
Phương pháp giải - Xem chi tiết
+ Tính thể tích V của khối gỗ hình trụ bán kính đáy bằng 1m, chiều cao bằng 2m.
+ Tính thể tích \({V_1}\) của hai nửa khối cầu bị khoét đi có bán kính 1m.
+ Tính thể tích phần còn lại của khối gỗ: \({V_2} = V - {V_1}\).
+ Tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ ban đầu là: \(\frac{{{V_2}}}{V}\).
Lời giải chi tiết
Thể tích của khối gỗ hình trụ là: \(V = \pi {.1^2}.2 = 2\pi \left( {{m^3}} \right)\).
Vì đường tròn đáy của hình trụ là đường tròn lớn của mỗi nửa hình cầu nên bán kính của mỗi nửa hình cầu là \(R = 1m\).
Thể tích của hai nửa khối cầu bị khoét đi là: \({V_1} = 2.\frac{1}{2}.\frac{4}{3}\pi {.1^3} = \frac{{4\pi }}{3}\left( {{m^3}} \right)\).
Thể tích phần còn lại của khối gỗ là: \({V_2} = V - {V_1} = 2\pi - \frac{{4\pi }}{3} = \frac{{2\pi }}{3}\left( {{m^3}} \right)\).
Tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ ban đầu là: \(\frac{{{V_2}}}{V} = \frac{{\frac{{2\pi }}{3}}}{{2\pi }} = \frac{1}{3}\).
Bài 10.19 sách bài tập Toán 9 Kết nối tri thức tập 2 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc hai. Cụ thể, bài toán thường mô tả một tình huống vật lý hoặc hình học, trong đó một đại lượng phụ thuộc vào một đại lượng khác theo một hàm số bậc hai. Để giải bài toán này, học sinh cần xác định được hàm số bậc hai mô tả mối quan hệ giữa các đại lượng, sau đó sử dụng các kiến thức về hàm số bậc hai để tìm ra giá trị cần tìm.
Bước đầu tiên để giải bài 10.19 là phân tích kỹ đề bài để hiểu rõ các thông tin đã cho và yêu cầu của bài toán. Sau đó, học sinh cần xác định được các đại lượng liên quan và mối quan hệ giữa chúng. Dựa trên các thông tin này, học sinh có thể xây dựng được hàm số bậc hai mô tả mối quan hệ giữa các đại lượng.
Ví dụ, nếu bài toán mô tả quỹ đạo của một vật được ném lên cao, thì hàm số bậc hai có thể mô tả mối quan hệ giữa chiều cao của vật và thời gian bay. Trong trường hợp này, chiều cao của vật là đại lượng phụ thuộc, thời gian bay là đại lượng độc lập, và hàm số bậc hai có dạng y = ax2 + bx + c, trong đó y là chiều cao của vật, x là thời gian bay, và a, b, c là các hệ số cần xác định.
Sau khi đã xác định được hàm số bậc hai, bước tiếp theo là tìm các hệ số a, b, c. Để làm điều này, học sinh cần sử dụng các thông tin đã cho trong đề bài để lập hệ phương trình và giải hệ phương trình đó. Thông thường, đề bài sẽ cung cấp một số điểm thuộc đồ thị của hàm số bậc hai, hoặc một số thông tin về các đặc điểm của đồ thị, chẳng hạn như đỉnh của đồ thị, trục đối xứng của đồ thị, hoặc giao điểm của đồ thị với các trục tọa độ.
Ví dụ, nếu đề bài cho biết đồ thị của hàm số bậc hai đi qua ba điểm A(x1, y1), B(x2, y2), C(x3, y3), thì học sinh có thể thay tọa độ của ba điểm này vào phương trình y = ax2 + bx + c để được ba phương trình bậc nhất theo a, b, c. Sau đó, học sinh có thể giải hệ ba phương trình này để tìm ra các giá trị của a, b, c.
Sau khi đã tìm được các hệ số của hàm số bậc hai, học sinh có thể sử dụng hàm số này để giải các bài toán liên quan. Các bài toán này có thể yêu cầu học sinh tìm giá trị của hàm số tại một điểm cho trước, tìm các điểm mà tại đó hàm số đạt giá trị lớn nhất hoặc nhỏ nhất, tìm giao điểm của đồ thị hàm số với các đường thẳng hoặc đường cong khác, hoặc giải các phương trình bậc hai.
Ví dụ, để tìm giá trị của hàm số tại một điểm x0, học sinh chỉ cần thay x = x0 vào phương trình y = ax2 + bx + c để tính ra giá trị tương ứng của y. Để tìm các điểm mà tại đó hàm số đạt giá trị lớn nhất hoặc nhỏ nhất, học sinh có thể sử dụng công thức tìm tọa độ đỉnh của parabol y = ax2 + bx + c, hoặc sử dụng phương pháp đạo hàm để tìm các điểm cực trị của hàm số.
Để nắm vững kiến thức về hàm số bậc hai và có thể giải thành thạo các bài toán liên quan, học sinh cần luyện tập thường xuyên và củng cố kiến thức. Giaitoan.edu.vn cung cấp một loạt các bài tập về hàm số bậc hai với nhiều mức độ khó khác nhau, giúp học sinh rèn luyện kỹ năng giải toán và nâng cao kiến thức. Ngoài ra, học sinh cũng có thể tham khảo các tài liệu học tập khác, chẳng hạn như sách giáo khoa, sách bài tập, và các trang web học toán trực tuyến.
Hy vọng rằng lời giải chi tiết và các hướng dẫn trên sẽ giúp các em học sinh hiểu rõ hơn về bài 10.19 trang 71 sách bài tập Toán 9 Kết nối tri thức tập 2 và tự tin giải các bài toán tương tự. Chúc các em học tập tốt!