Bài 7.26 thuộc chương trình Toán 9 Kết nối tri thức tập 2, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này thường gặp trong các kỳ thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
Biểu đồ hình quạt tròn sau đây cho biết tỉ lệ vô địch bóng đá nam SEA Games của các đội bóng trong khu vực tính đến năm 2023. (Theo Liên đoàn bóng đá Đông Nam Á) a) Lập bảng tần số tương đối cho biết tỉ lệ vô địch bóng đá nam SEA Games của các đội bóng trong khu vực. b) Biết rằng tính đến năm 2023 môn Bóng đá nam đã được tổ chức ở 32 kì SEA Games. Lập bảng tần số cho số lần vô địch của các đội tuyển (làm tròn số liệu đến số nguyên gần nhất). c) Vẽ biểu đồ tần số dạng cột biểu diễn bảng tần s
Đề bài
Biểu đồ hình quạt tròn sau đây cho biết tỉ lệ vô địch bóng đá nam SEA Games của các đội bóng trong khu vực tính đến năm 2023.
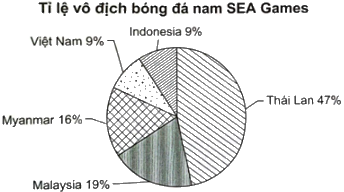
(Theo Liên đoàn bóng đá Đông Nam Á)
a) Lập bảng tần số tương đối cho biết tỉ lệ vô địch bóng đá nam SEA Games của các đội bóng trong khu vực.
b) Biết rằng tính đến năm 2023 môn Bóng đá nam đã được tổ chức ở 32 kì SEA Games. Lập bảng tần số cho số lần vô địch của các đội tuyển (làm tròn số liệu đến số nguyên gần nhất).
c) Vẽ biểu đồ tần số dạng cột biểu diễn bảng tần số thu được ở câu b.
d) Đội tuyển quốc gia nào có số lần vô địch bóng đá nam SEA Games nhiều nhất, với bao nhiêu lần?
Phương pháp giải - Xem chi tiết
a) Lập bảng tần số tương đối:
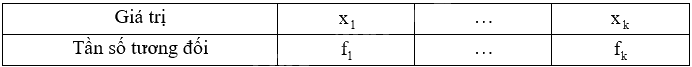
Trong đó, giá trị \({x_i}\) có tần số tương đối là \({f_i}\).
b) + Tần số của số lần vô địch của đội tuyển= tỉ lệ vô địch. 32.
+ Bảng tần số có dạng bảng sau:

Trong đó, \({m_1}\) là tần số của \({x_1}\), \({m_2}\) là tần số của \({x_2}\),…, \({m_k}\) là tần số của \({x_k}\).
c) Cách vẽ biểu đồ cột:
+ Vẽ hai trục ngang và dọc vuông góc với nhau, trục ngang biểu thị các giá trị trong dãy dữ liệu, trục đứng: chọn khoảng chia thích hợp với dữ liệu và ghi ở các vạch chia.
+ Tại các vị trí đối tượng trên trục ngang, vẽ các cột hình chữ nhật: cách đều nhau, có cùng chiều rộng và chiều cao thể hiện mức tăng trưởng của khu vực kinh tế, tương ứng với khoảng chia trên trục dọc.
+ Ghi chú giải cho các trục, các điểm và tiêu đề của biểu đồ.
d) Đội tuyển nào có tần số lớn nhất thì vô địch nhiều lần nhất.
Lời giải chi tiết
a) Bảng tần số tương đối:

b) Số lần vô địch của đội tuyển Thái Lan là: \(32.47\% \approx 15\) (lần).
Số lần vô địch của đội tuyển Malaysia là: \(32.19\% \approx 6\) (lần).
Số lần vô địch của đội tuyển Myanmar là: \(32.16\% \approx 5\) (lần).
Số lần vô địch của đội tuyển Việt Nam là: \(32.9\% \approx 3\) (lần).
Số lần vô địch của đội tuyển Indonesia là: \(32.9\% \approx 3\) (lần).
Bảng tần số:

c) Biểu đồ tần số dạng cột:
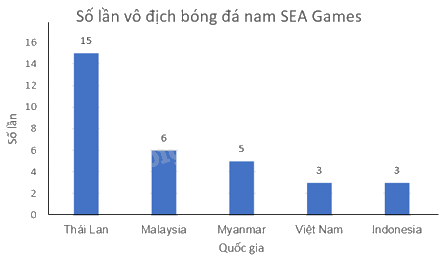
d) Thái Lan là đội bóng vô địch nhiều nhất với 15 lần.
Bài 7.26 sách bài tập Toán 9 Kết nối tri thức tập 2 là một bài toán ứng dụng thực tế về hàm số bậc hai. Để giải bài toán này, học sinh cần nắm vững các kiến thức sau:
Trước khi bắt tay vào giải bài toán, học sinh cần đọc kỹ đề bài, phân tích các thông tin đã cho và xác định yêu cầu của bài toán. Điều này giúp học sinh có cái nhìn tổng quan về bài toán và lựa chọn phương pháp giải phù hợp.
(Ở đây sẽ là lời giải chi tiết của bài toán, bao gồm các bước giải, giải thích rõ ràng và minh họa bằng hình ảnh nếu cần thiết. Lời giải sẽ được trình bày một cách logic và dễ hiểu, giúp học sinh nắm bắt được phương pháp giải bài toán.)
Để giúp học sinh hiểu rõ hơn về phương pháp giải bài toán, chúng tôi sẽ cung cấp một số ví dụ minh họa và bài tập tương tự. Học sinh có thể tự giải các bài tập này để củng cố kiến thức và rèn luyện kỹ năng.
Hàm số bậc hai có rất nhiều ứng dụng trong thực tế, từ việc tính toán quỹ đạo của vật thể đến việc tối ưu hóa lợi nhuận. Việc nắm vững kiến thức về hàm số bậc hai sẽ giúp học sinh giải quyết các bài toán thực tế một cách hiệu quả.
Bài 7.26 sách bài tập Toán 9 Kết nối tri thức tập 2 là một bài toán ứng dụng thực tế về hàm số bậc hai. Để giải bài toán này, học sinh cần nắm vững các kiến thức về hàm số bậc hai, phương trình bậc hai và ứng dụng của hàm số bậc hai. Hy vọng với lời giải chi tiết và các ví dụ minh họa, học sinh sẽ hiểu rõ hơn về phương pháp giải bài toán và tự tin giải các bài tập tương tự.