Bài 10.15 trang 70 sách bài tập Toán 9 Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 10.15 trang 70 SBT Toán 9, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Một chiếc nón lá có dạng một hình nón không có đáy, đường kính đáy bằng 80cm, chiều cao bằng 30cm. Tính diện tích mặt ngoài của chiếc nón (làm tròn kết quả đến hàng đơn vị của (c{m^2})).
Đề bài
Một chiếc nón lá có dạng một hình nón không có đáy, đường kính đáy bằng 80cm, chiều cao bằng 30cm. Tính diện tích mặt ngoài của chiếc nón (làm tròn kết quả đến hàng đơn vị của \(c{m^2}\)).
Phương pháp giải - Xem chi tiết
Diện tích xung quanh của hình nón bán kính đáy r và độ dài đường sinh l là: \({S_{xq}} = \pi rl\).
Lời giải chi tiết
Đặt tên các điểm như hình vẽ.
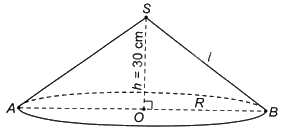
Bán kính đáy của hình nón là: \(R = OB = 80:2 = 40\left( {cm} \right)\).
Tam giác SOB vuông tại O nên theo định lí Pythagore ta có:
\(S{B^2} = S{O^2} + O{B^2} = 2\;500\) nên \(SB = 50m\).
Diện tích mặt ngoài của hình nón là:
\({S_{xq}} = \pi .OB.SB = 40.50.\pi = 2\;000\pi \left( {c{m^2}} \right) \approx 6\;283c{m^2}.\)
Bài 10.15 sách bài tập Toán 9 Kết nối tri thức tập 2 yêu cầu chúng ta giải một bài toán liên quan đến hàm số bậc hai và ứng dụng thực tế. Để giải bài này, chúng ta cần nắm vững các kiến thức sau:
Trước khi bắt đầu giải bài, chúng ta cần đọc kỹ đề bài và xác định yêu cầu của bài toán. Trong bài 10.15, đề bài yêu cầu chúng ta tìm các thông số của hàm số bậc hai dựa trên các thông tin đã cho. Cụ thể, chúng ta cần xác định hệ số a, b, và c của hàm số y = ax2 + bx + c.
Để giải bài 10.15, chúng ta sẽ thực hiện các bước sau:
Ví dụ minh họa:
Giả sử đề bài cho biết đồ thị hàm số đi qua các điểm A(0; 1), B(1; 2), và C(-1; 0). Chúng ta sẽ thay tọa độ các điểm này vào phương trình y = ax2 + bx + c:
Thay c = 1 vào hai phương trình còn lại, ta được:
Giải hệ phương trình này, ta được:
Vậy phương trình hàm số bậc hai là y = 0x2 + 1x + 1, hay y = x + 1.
Khi giải bài tập về hàm số bậc hai, các em cần lưu ý những điều sau:
Để củng cố kiến thức về hàm số bậc hai, các em có thể tự giải các bài tập tương tự sau:
Giaitoan.edu.vn hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về bài 10.15 trang 70 SBT Toán 9 - Kết nối tri thức tập 2 và tự tin hơn trong quá trình học tập.