Bài 5.6 trang 59 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hệ phương trình bậc nhất hai ẩn để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5.6 trang 59, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho tam giác nhọn ABC, hai đường cao BD và CE cắt nhau tại H. Chứng minh rằng: a) Bốn điểm A, E, H, D cùng thuộc một đường tròn. b) (AH > DE).
Đề bài
Cho tam giác nhọn ABC, hai đường cao BD và CE cắt nhau tại H. Chứng minh rằng:
a) Bốn điểm A, E, H, D cùng thuộc một đường tròn.
b) \(AH > DE\).
Phương pháp giải - Xem chi tiết
a) + Gọi I là trung điểm của AB.
+ Chứng minh \(IA = ID = IH = IE = \frac{1}{2}AH\) nên bốn điểm A, E, H, D cùng thuộc đường tròn tâm I đường kính AH.
b) Vì góc EAD là góc nhọn nên dây DE là dây không đi qua tâm của đường tròn tâm I đường kính AH nên \(AH > DE\).
Lời giải chi tiết
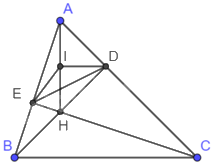
a) Gọi I là trung điểm của AH.
Vì BD và CE là hai đường cao của tam giác ABC nên \(BD \bot AC\) tại D, \(CE \bot AB\) tại E.
Do đó, tam giác AEH vuông tại E và tam giác ADH vuông tại D.
Tam giác AEH vuông tại E, có EI là đường trung tuyến nên \(IA = IE = IH = \frac{1}{2}AH\left( 1 \right)\)
Tam giác ADH vuông tại D, có DI là đường trung tuyến nên \(IA = ID = IH = \frac{1}{2}AH\left( 2 \right)\)
Từ (1) và (2) ta có: \(IA = ID = IH = IE = \frac{1}{2}AH\). Do đó, bốn điểm A, E, H, D cùng thuộc đường tròn tâm I đường kính AH.
b) Vì góc EAD là góc nhọn nên dây DE là dây không đi qua tâm của đường tròn đường kính AH nên \(AH > DE\).
Bài 5.6 trang 59 sách bài tập Toán 9 - Kết nối tri thức tập 1 yêu cầu giải bài toán về việc tìm hai số khi biết tổng và hiệu của chúng. Bài toán thường được trình bày dưới dạng một tình huống thực tế, đòi hỏi học sinh phải chuyển đổi thông tin thành hệ phương trình để giải.
Để giải bài toán này, chúng ta sẽ sử dụng phương pháp giải hệ phương trình bậc nhất hai ẩn. Có ba phương pháp phổ biến:
Đề bài: (Giả sử đề bài là: Hai số có tổng là 10 và hiệu là 4. Tìm hai số đó.)
Giải:
Gọi hai số cần tìm là x và y. Theo đề bài, ta có hệ phương trình:
Sử dụng phương pháp cộng đại số:
Cộng hai phương trình lại, ta được:
(x + y) + (x - y) = 10 + 4
2x = 14
x = 7
Thay x = 7 vào phương trình x + y = 10, ta được:
7 + y = 10
y = 3
Vậy hai số cần tìm là 7 và 3.
Các bài tập tương tự bài 5.6 thường có dạng:
Khi giải các bài tập này, cần chú ý:
Ví dụ: Một người có tất cả 30 con gà và thỏ. Biết rằng số chân của chúng là 84. Hỏi người đó có bao nhiêu con gà, bao nhiêu con thỏ?
Giải:
Gọi số gà là x, số thỏ là y. Ta có hệ phương trình:
Giải hệ phương trình này, ta tìm được x = 18 và y = 12.
Vậy người đó có 18 con gà và 12 con thỏ.
Để nắm vững kiến thức về hệ phương trình bậc nhất hai ẩn, các em học sinh nên luyện tập thêm các bài tập khác trong sách bài tập và các nguồn tài liệu khác. Giaitoan.edu.vn sẽ cung cấp thêm nhiều bài tập và lời giải chi tiết trong các bài viết tiếp theo.
Bài 5.6 trang 59 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải hệ phương trình bậc nhất hai ẩn. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ hiểu rõ hơn về bài toán này và tự tin làm bài tập.