Bài 14 trang 73 Sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học Toán 9. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 14 trang 73 Sách bài tập Toán 9 - Kết nối tri thức tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho tam giác ABC nội tiếp đường tròn (O), vẽ (AX bot BC) và cắt nhau tại điểm D. Cho điểm H trên đoạn thẳng AD sao cho (DH = DX). Cho BH cắt AC tại E và CH cắt AB tại F. a) Chứng minh rằng H là trực tâm của tam giác ABC. b) Chứng minh rằng H là tâm của đường tròn nội tiếp tam giác DEF.
Đề bài
Cho tam giác ABC nội tiếp đường tròn (O), vẽ \(AX \bot BC\) và cắt nhau tại điểm D. Cho điểm H trên đoạn thẳng AD sao cho \(DH = DX\). Cho BH cắt AC tại E và CH cắt AB tại F.
a) Chứng minh rằng H là trực tâm của tam giác ABC.
b) Chứng minh rằng H là tâm của đường tròn nội tiếp tam giác DEF.
Phương pháp giải - Xem chi tiết
a) + Chứng minh \(\Delta BDH = \Delta BDX\left( {c.g.c} \right)\)nên \(\widehat {HBD} = \widehat {DBX}\).
+ Mà \(\widehat {CBX} = \widehat {CAX}\) nên \(\widehat {HBD} = \widehat {CAX} = {90^o} - \widehat {ACB}\).
+ Chứng minh \(\widehat {BEC} = {90^o}\). Do đó, \(BE \bot AC\).
+ Chứng minh tương tự ta có: \(CF \bot AB\).
+ Do đó, H là trực tâm của tam giác ABC.
b) + Chứng minh tứ giác HDBF nội tiếp đường tròn đường kính BH, suy ra \(\widehat {HDF} = \widehat {HBF}\).
+ Tương tự ta có: \(\widehat {HDE} = \widehat {HCE}\). Mà \(\widehat {HBF} = {90^o} - \widehat {BAC} = \widehat {HCE}\) nên \(\widehat {HDF} = \widehat {HBF} = \widehat {HCE} = \widehat {HDE}\), suy ra H nằm trên đường phân giác của góc EDF của tam giác DEF.
+ Tương tự ta có: H nằm trên các đường phân giác của các góc DEF, DFE. Do đó, H là tâm đường tròn nội tiếp tam giác DEF.
Lời giải chi tiết
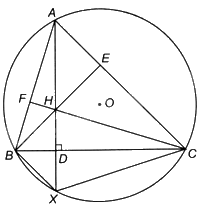
a) Tam giác BDH và tam giác BDX có: BD là cạnh chung, \(\widehat {BDH} = \widehat {BDX} = {90^o},DH = DX\) nên \(\Delta BDH = \Delta BDX\left( {c.g.c} \right)\), suy ra \(\widehat {HBD} = \widehat {DBX}\).
Mặt khác \(\widehat {CBX} = \widehat {CAX}\) (hai góc nội tiếp (O) cùng chắn cung CX). Do đó, \(\widehat {HBD} = \widehat {CAX} = {90^o} - \widehat {ACB}\).
Tam giác BEC có: \(\widehat {BEC} = {180^o} - \widehat {EBC} - \widehat {ACB} = {180^o} - {90^o} + \widehat {ACB} - \widehat {ACB} = {90^o}\). Do đó, \(BE \bot AC\).
Chứng minh tương tự ta có: \(CF \bot AB\). Do đó, H là trực tâm của tam giác ABC.
b) Do \(\widehat {HDB} = \widehat {HFB} = {90^o}\) nên tứ giác HDBF nội tiếp đường tròn đường kính BH.
Do đó, \(\widehat {HDF} = \widehat {HBF}\) (hai góc nội tiếp cùng chắn cung HF của đường tròn đường kính BH).
Tương tự ta có: \(\widehat {HDE} = \widehat {HCE}\).
Mặt khác, \(\widehat {HBF} = {90^o} - \widehat {BAC} = \widehat {HCE}\).
Do đó, \(\widehat {HDF} = \widehat {HBF} = \widehat {HCE} = \widehat {HDE}\). Vậy H nằm trên đường phân giác của góc EDF của tam giác DEF.
Tương tự, H nằm trên các đường phân giác của các góc DEF, DFE. Do đó, H là tâm đường tròn nội tiếp tam giác DEF.
Bài 14 trang 73 Sách bài tập Toán 9 - Kết nối tri thức tập 2 thuộc chương trình học về hàm số bậc nhất và hàm số bậc hai. Bài tập này thường yêu cầu học sinh xác định hệ số góc, đường thẳng song song, vuông góc, và ứng dụng vào giải quyết các bài toán liên quan đến thực tế.
Bài 14 thường bao gồm các dạng bài tập sau:
Bài 14: Cho hai đường thẳng d1: y = 2x - 1 và d2: y = -x + 3. Tìm giao điểm của hai đường thẳng này.
Lời giải:
y = 2x - 1
y = -x + 3
Ngoài sách giáo khoa và sách bài tập, các em có thể tham khảo thêm các tài liệu sau:
Bài 14 trang 73 Sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về hàm số bậc nhất và bậc hai. Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, các em sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.