Bài 4.23 trang 49 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.23 trang 49, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
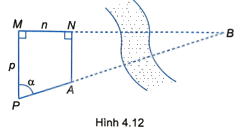
Cho A, B là hai địa điểm ở hai bên bờ sông, biết AN và PM cùng vuông góc MN, (MN = n) (mét), (MP = p) (mét), (p > n) và (widehat {MPA} = alpha ) (H.4.12). Chứng minh rằng: (AB = frac{{ptan alpha - n}}{{sin alpha }}).
Đề bài
Cho A, B là hai địa điểm ở hai bên bờ sông, biết AN và PM cùng vuông góc MN, \(MN = n\) (mét), \(MP = p\) (mét), \(p > n\) và \(\widehat {MPA} = \alpha \) (H.4.12). Chứng minh rằng: \(AB = \frac{{p\tan \alpha - n}}{{\sin \alpha }}\).
Phương pháp giải - Xem chi tiết
+ Chứng minh \(\widehat {BAN} = \widehat {BPM} = \alpha \).
+ Tam giác BAN vuông tại N có: \(BN = AB.\sin \alpha \).
+ Tam giác BPM vuông tại M có: \(BM = PM\tan \alpha = p\tan \alpha \).
+ \(BM - BN = MN = n\) nên \(p\tan \alpha - AB\sin \alpha = n\), từ đó tính được AB theo n, p, \(\alpha \).
Lời giải chi tiết
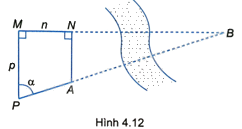
Vì AN//PM nên \(\widehat {BAN} = \widehat {BPM} = \alpha \).
Tam giác BAN vuông tại N có:
\(BN = AB.\sin \alpha \).
Tam giác BPM vuông tại M có:
\(BM = PM\tan \alpha = p\tan \alpha \).
Vì \(BM - BN = MN = n\) nên \(p\tan \alpha - AB\sin \alpha = n\).
Suy ra \(AB = \frac{{p\tan \alpha - n}}{{\sin \alpha }}\).
Bài 4.23 trang 49 sách bài tập Toán 9 - Kết nối tri thức tập 1 thuộc chương Hàm số bậc nhất và hàm số bậc hai. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Đề bài: (Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho hàm số y = 2x + 3. Tìm giá trị của x khi y = 7.)
Lời giải:
Kết luận: (Ví dụ: Vậy, khi y = 7 thì x = 2.)
Để hiểu rõ hơn về cách giải bài 4.23, chúng ta cùng xem xét một số ví dụ minh họa sau:
Ví dụ 1: (Đề bài và lời giải tương tự)
Ví dụ 2: (Đề bài và lời giải tương tự)
Ngoài ra, các em có thể tự luyện tập với các bài tập tương tự sau:
Để giải các bài tập về hàm số bậc nhất và bậc hai một cách hiệu quả, các em nên lưu ý những mẹo sau:
Bài 4.23 trang 49 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng giúp các em củng cố kiến thức về hàm số bậc nhất và bậc hai. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em sẽ tự tin hơn khi giải các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!