Bài 10.13 trang 69 sách bài tập Toán 9 Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các vấn đề thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 10.13 trang 69 SBT Toán 9, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
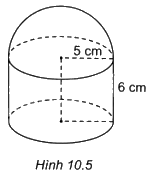
Một hộp đựng mĩ phẩm được thiết kế thân hộp có dạng hình trụ, nắp hộp có dạng nửa hình cầu với kích thước như Hình 10.5. Nếu sơn bên ngoài vỏ hộp (không sơn đáy) thì diện tích cần sơn là bao nhiêu?
Đề bài
Một hộp đựng mĩ phẩm được thiết kế thân hộp có dạng hình trụ, nắp hộp có dạng nửa hình cầu với kích thước như Hình 10.5. Nếu sơn bên ngoài vỏ hộp (không sơn đáy) thì diện tích cần sơn là bao nhiêu?
Phương pháp giải - Xem chi tiết
Diện tích vỏ hộp cần sơn bằng tổng nửa diện tích mặt cầu bán kính 5cm và diện tích xung quanh hình trụ bán kính đáy 5cm và chiều cao 6cm.
Lời giải chi tiết
Diện tích vỏ hộp cần sơn là:
\(S = \frac{1}{2}.4\pi {R^2} + 2\pi Rh = \frac{1}{2}.4\pi {.5^2} + 2\pi .5.6 = 110\pi \left( {c{m^2}} \right).\)
Bài 10.13 trang 69 sách bài tập Toán 9 Kết nối tri thức tập 2 yêu cầu học sinh giải bài toán liên quan đến hàm số bậc hai và ứng dụng của nó trong việc mô tả các hiện tượng thực tế. Cụ thể, đề bài thường cho một tình huống thực tế và yêu cầu học sinh xây dựng hàm số bậc hai phù hợp, sau đó tìm các giá trị cần thiết để giải quyết vấn đề.
Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức sau:
(Ở đây sẽ là lời giải chi tiết của bài toán 10.13, bao gồm các bước giải, giải thích rõ ràng và các kết luận chính. Lời giải sẽ được trình bày chi tiết, dễ hiểu, phù hợp với trình độ của học sinh lớp 9. Ví dụ:)
Ví dụ: Giả sử đề bài yêu cầu tìm chiều cao tối đa của một quả bóng được ném lên không trung theo hàm số h(t) = -5t2 + 20t.
Ngoài bài 10.13, sách bài tập Toán 9 Kết nối tri thức tập 2 còn nhiều bài tập tương tự về hàm số bậc hai. Để giải tốt các bài tập này, học sinh cần luyện tập thường xuyên và nắm vững các kiến thức cơ bản. Một số dạng bài tập thường gặp:
Để giải bài tập hàm số bậc hai nhanh chóng và hiệu quả, học sinh có thể áp dụng một số mẹo sau:
Bài 10.13 trang 69 sách bài tập Toán 9 Kết nối tri thức tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.