Bài 4.7 trang 45 sách bài tập toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng trong chương trình học toán lớp 9. Bài tập này yêu cầu học sinh vận dụng kiến thức về hệ phương trình bậc nhất hai ẩn để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.7 trang 45 sách bài tập toán 9 - Kết nối tri thức tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Xét tam giác ABC vuông tại B, có (widehat A = {30^o}). Tia Bt sao cho (widehat {CBt} = {30^o}) cắt tia AC ở D, D nằm giữa A và C. Chứng minh rằng khoảng cách từ D đến đường thẳng BC bằng (frac{{AB}}{4}).
Đề bài
Xét tam giác ABC vuông tại B, có \(\widehat A = {30^o}\). Tia Bt sao cho \(\widehat {CBt} = {30^o}\) cắt tia AC ở D, D nằm giữa A và C. Chứng minh rằng khoảng cách từ D đến đường thẳng BC bằng \(\frac{{AB}}{4}\).
Phương pháp giải - Xem chi tiết
+ Tam giác ABC vuông tại B, \(\widehat A = {30^o}\) nên tính được góc C.
+ Tính góc BDC từ đó suy ra tam giác BDC vuông tại D, suy ra \(\frac{{BD}}{{AB}} = \sin \widehat {BAD}\).
+ Gọi E là chân đường vuông góc kẻ từ D lên BC thì DE là khoảng cách từ D đến đường thẳng BC.
+ Tam giác BDE vuông tại E nên \(\frac{{DE}}{{BD}} = \sin \widehat {DBE}\).
+ Ta có: \(\frac{{DE}}{{AB}} = \frac{{DE}}{{BD}}.\frac{{BD}}{{AB}}\), từ đó tính được \(DE = \frac{{AB}}{4}\).
Lời giải chi tiết
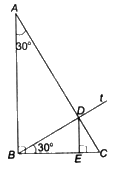
Tam giác ABC vuông tại B nên \(\widehat C = {90^o} - \widehat A = {60^o}\).
Tam giác BCD có: \(\widehat {BDC} = {180^o} - \widehat {DBC} - \widehat C = {90^o}\). Do đó, tam giác BCD vuông tại D.
Suy ra, \(\frac{{BD}}{{AB}} = \sin \widehat {BAD} = \sin {30^o} = \frac{1}{2}\)
Gọi E là chân đường vuông góc kẻ từ D lên BC thì DE là khoảng cách từ D đến đường thẳng BC.
Trong tam giác BDE vuông tại E có: \(\frac{{DE}}{{BD}} = \sin \widehat {DBE} = \sin {30^o} = \frac{1}{2}\)
Ta có: \(\frac{{DE}}{{AB}} = \frac{{DE}}{{BD}}.\frac{{BD}}{{AB}} = \frac{1}{2}.\frac{1}{2} = \frac{1}{4}\), suy ra \(DE = \frac{{AB}}{4}\).
Bài 4.7 trang 45 sách bài tập toán 9 - Kết nối tri thức tập 1 thuộc chương trình học toán lớp 9, tập trung vào việc ứng dụng hệ phương trình bậc nhất hai ẩn vào giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:
Bài 4.7 yêu cầu giải một bài toán thực tế liên quan đến việc tìm hai số khi biết tổng và hiệu của chúng, hoặc biết tổng và tích của chúng. Bài toán thường được trình bày dưới dạng một tình huống cụ thể, đòi hỏi học sinh phải phân tích và chuyển đổi thông tin để lập được hệ phương trình phù hợp.
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 4.7 trang 45 sách bài tập toán 9 - Kết nối tri thức tập 1, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể:
Một người đi xe máy từ A đến B với vận tốc 40km/h. Sau khi đi được 1 giờ, người đó tăng vận tốc lên 50km/h và đến B muộn hơn 30 phút so với dự kiến. Tính quãng đường AB.
Giải:
Giải phương trình trên, ta được x = 200.
Ngoài bài 4.7, sách bài tập toán 9 - Kết nối tri thức tập 1 còn nhiều bài tập tương tự khác. Các em học sinh có thể luyện tập thêm các bài tập sau để củng cố kiến thức:
Để giải các bài tập hệ phương trình một cách nhanh chóng và chính xác, các em học sinh có thể tham khảo một số mẹo sau:
Để học toán 9 hiệu quả hơn, các em học sinh có thể tham khảo thêm các tài liệu sau:
Bài 4.7 trang 45 sách bài tập toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải hệ phương trình và ứng dụng vào giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc học toán 9.