Bài 7.22 trang 37 Sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học Toán 9. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.22 trang 37 Sách bài tập Toán 9 - Kết nối tri thức tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Bảng thống kê sau cho biết thời gian học tiếng Anh (đơn vị là năm, tính từ lúc bắt đầu học tiếng Anh đến thời điểm khảo sát) của một số học sinh lớp 9. a) Lập bảng tần số tương đối ghép nhóm cho bảng thống kê trên. b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng cột biểu diễn bảng tần số tương đối ghép nhóm thu được ở câu a.
Đề bài
Bảng thống kê sau cho biết thời gian học tiếng Anh (đơn vị là năm, tính từ lúc bắt đầu học tiếng Anh đến thời điểm khảo sát) của một số học sinh lớp 9.

a) Lập bảng tần số tương đối ghép nhóm cho bảng thống kê trên.
b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng cột biểu diễn bảng tần số tương đối ghép nhóm thu được ở câu a.
Phương pháp giải - Xem chi tiết
a) + Tính tần số tương đối ứng với các giá trị trong mẫu dữ liệu: Nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\) có tần số \({m_i}\) thì có tần số tương đối là: \({f_i} = \frac{{{m_i}}}{n}.100\left( \% \right)\) với m là tổng tất cả các tần số có trong mẫu số liệu.
+ Lập bảng tần số tương đối ghép nhóm:

b) Cách vẽ biểu đồ tần số tương đối ghép nhóm dạng cột:
Bước 1: Vẽ trục đứng, trục ngang. Trên trục đứng xác định đơn vị độ dài phù hợp với các tần số tương đối. Trên trục ngang xác định các nhóm số liệu cần biểu diễn.
Bước 2: Dựng các hình cột (kề nhau) ứng với các nhóm dữ liệu, mỗi hình cột có chiều cao bằng tần số tương đối của nhóm số liệu.
Bước 3: Ghi chú giải cho các trục, các cột và tiêu đề cho biểu đồ.
Lời giải chi tiết
a) Tổng số học sinh là: \(8 + 12 + 15 + 10 + 5 = 50\).
Tần số tương đối của các nhóm [0; 2), [2; 4), [4; 6), [6; 8), [8; 10) lần lượt là:
\(\frac{8}{{50}}.100\% = 16\% ;\frac{{12}}{{50}}.100\% = 24\% ;\frac{{15}}{{50}}.100\% = 30\% ;\\\frac{{10}}{{50}}.100\% = 20\% ;\frac{5}{{50}}.100\% = 10\% \)
Bảng tần số tương đối ghép nhóm:

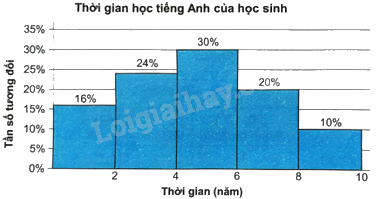
b) Biểu đồ tần số tương đối ghép nhóm:
Bài 7.22 trang 37 Sách bài tập Toán 9 - Kết nối tri thức tập 2 thuộc chương Hàm số bậc nhất và hàm số bậc hai. Bài toán này thường yêu cầu học sinh xác định hệ số góc, điểm cắt trục, và ứng dụng hàm số để giải quyết các bài toán liên quan đến thực tế.
Trước khi bắt đầu giải bài, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu. Xác định các thông tin đã cho và những gì cần tìm. Ví dụ, đề bài có thể yêu cầu tìm phương trình đường thẳng đi qua hai điểm, hoặc xác định giao điểm của hai đường thẳng.
Để giải bài 7.22 trang 37, học sinh cần nắm vững các kiến thức sau:
(Ở đây sẽ là lời giải chi tiết của bài toán, bao gồm các bước giải, giải thích rõ ràng và các ví dụ minh họa. Lời giải sẽ được trình bày chi tiết, dễ hiểu, phù hợp với trình độ của học sinh lớp 9.)
Ví dụ, nếu bài toán yêu cầu tìm phương trình đường thẳng đi qua hai điểm A(x1, y1) và B(x2, y2), ta có thể sử dụng công thức:
(y - y1) / (x - x1) = (y2 - y1) / (x2 - x1)
Sau khi tìm được phương trình đường thẳng, ta có thể thay các giá trị x để tìm các điểm thuộc đường thẳng đó.
Ngoài bài 7.22, còn rất nhiều bài tập tương tự trong chương Hàm số bậc nhất và hàm số bậc hai. Để làm tốt các bài tập này, học sinh cần luyện tập thường xuyên và nắm vững các kiến thức cơ bản.
Một số dạng bài tập thường gặp:
Để giải bài tập hàm số bậc nhất và bậc hai một cách hiệu quả, học sinh có thể áp dụng một số mẹo sau:
Bài 7.22 trang 37 Sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và hàm số bậc hai. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải bài tập này và các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!