Bài 8.15 trang 48 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hệ phương trình bậc nhất hai ẩn để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8.15 trang 48, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Bạn Tuấn viết ba bức thu cho ba người bạn An, Bình, Cường và viết tên, địa chỉ của ba người đó lên ba chiếc phong bì. Xếp ngẫu nhiên ba bức thư đó vào ba phong bì. a) Mô tả không gian mẫu của phép thử. b) Tính xác suất của các biến cố sau: • E: “Có đúng một bức thư đúng địa chỉ”; • F: “Cả ba bức thư đúng địa chỉ”; • G: “Không có bức thư nào đúng địa chỉ”; • H: “Có ít nhất một bức thư đúng địa chỉ”.
Đề bài
Bạn Tuấn viết ba bức thu cho ba người bạn An, Bình, Cường và viết tên, địa chỉ của ba người đó lên ba chiếc phong bì. Xếp ngẫu nhiên ba bức thư đó vào ba phong bì.
a) Mô tả không gian mẫu của phép thử.
b) Tính xác suất của các biến cố sau:
E: “Có đúng một bức thư đúng địa chỉ”;
F: “Cả ba bức thư đúng địa chỉ”;
G: “Không có bức thư nào đúng địa chỉ”;
H: “Có ít nhất một bức thư đúng địa chỉ”.
Phương pháp giải - Xem chi tiết
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết
a) Mô tả không gian mẫu:
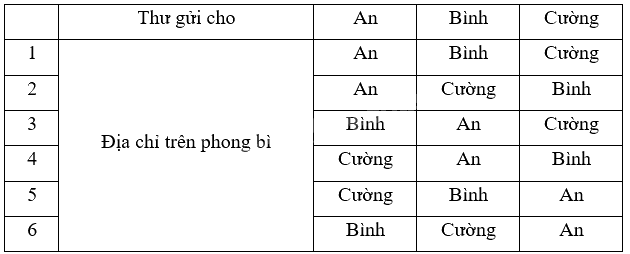
Không gian mẫu có 6 kết quả có thể là 6 dòng ở bảng trên.
b) Có 3 kết quả thuận lợi cho biến cố E là kết quả 2 (chỉ có An đúng), kết quả 3 (chỉ có Cường đúng) và kết quả 5 (chỉ có Bình đúng).
Do đó, \(P\left( E \right) = \frac{3}{6} = \frac{1}{2}\).
Có 1 kết quả thuận lợi cho biến cố F là kết quả 1.
Do đó, \(P\left( F \right) = \frac{1}{6}\).
Có 2 kết quả thuận lợi cho biến cố G là kết quả 4, kết quả 6.
Do đó, \(P\left( G \right) = \frac{2}{6} = \frac{1}{3}\).
Có 4 kết quả thuận lợi cho biến cố H là kết quả 1, kết quả 2, kết quả 3, kết quả 5.
Do đó, \(P\left( H \right) = \frac{4}{6} = \frac{2}{3}\)
Bài 8.15 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài toán ứng dụng thực tế, yêu cầu học sinh sử dụng kiến thức về hệ phương trình bậc nhất hai ẩn để giải quyết. Dưới đây là đề bài và lời giải chi tiết:
Đề bài:
Một người đi xe máy từ A đến B với vận tốc 40 km/h. Sau khi đến B, người đó nghỉ lại 15 phút rồi quay về A với vận tốc 30 km/h. Thời gian cả đi lẫn về là 4 giờ 30 phút. Tính độ dài quãng đường AB.
Lời giải:
Gọi x là độ dài quãng đường AB (km).
Thời gian đi từ A đến B là: x/40 (giờ)
Thời gian đi từ B về A là: x/30 (giờ)
Thời gian nghỉ lại ở B là: 15 phút = 1/4 giờ
Tổng thời gian cả đi lẫn về là 4 giờ 30 phút = 4.5 giờ
Ta có phương trình:
x/40 + x/30 + 1/4 = 4.5
Quy đồng mẫu số:
3x/120 + 4x/120 + 30/120 = 540/120
7x + 30 = 540
7x = 510
x = 510/7 ≈ 72.86 (km)
Vậy độ dài quãng đường AB là khoảng 72.86 km.
Để giải bài toán này, chúng ta cần nắm vững các bước sau:
Hệ phương trình bậc nhất hai ẩn là một công cụ quan trọng trong việc giải quyết các bài toán thực tế. Ngoài bài toán trên, hệ phương trình còn được ứng dụng trong nhiều lĩnh vực khác như kinh tế, vật lý, hóa học,...
Để hiểu rõ hơn về hệ phương trình bậc nhất hai ẩn, các em có thể tham khảo thêm các tài liệu sau:
Để củng cố kiến thức về hệ phương trình bậc nhất hai ẩn, các em nên luyện tập thêm các bài toán tương tự. Dưới đây là một số bài tập gợi ý:
Bài 8.15 trang 48 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài toán ứng dụng thực tế, giúp các em học sinh rèn luyện kỹ năng giải hệ phương trình bậc nhất hai ẩn. Hy vọng với lời giải chi tiết và các kiến thức mở rộng trên, các em sẽ hiểu rõ hơn về bài toán này và tự tin làm bài tập.