Bài 8.14 trang 48 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8.14 trang 48, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Trong một trò chơi, có hai bánh xe, mỗi bánh xe được gắn vào trục quay có mũi tên ở tâm. Bánh xe thứ nhất được chia làm bốn hình quạt như nhau và sơn các màu: trắng, đỏ, xanh, vàng. Bánh xe thứ hai được chia làm ba hình quạt như nhau và sơn các màu: đỏ, xanh, vàng. Người chơi quay hai bánh xe. Người chơi đạt giải nhất nếu hai mũi tên dừng lại ở hai hình quạt màu đỏ, đạt giải nhì nếu hai mũi tên dừng lại ở hai hình quạt cùng màu và đạt giải ba nếu có đúng một mũi tên dừng ở hình quạt màu đỏ. Tính
Đề bài
Trong một trò chơi, có hai bánh xe, mỗi bánh xe được gắn vào trục quay có mũi tên ở tâm. Bánh xe thứ nhất được chia làm bốn hình quạt như nhau và sơn các màu: trắng, đỏ, xanh, vàng. Bánh xe thứ hai được chia làm ba hình quạt như nhau và sơn các màu: đỏ, xanh, vàng. Người chơi quay hai bánh xe. Người chơi đạt giải nhất nếu hai mũi tên dừng lại ở hai hình quạt màu đỏ, đạt giải nhì nếu hai mũi tên dừng lại ở hai hình quạt cùng màu và đạt giải ba nếu có đúng một mũi tên dừng ở hình quạt màu đỏ. Tính xác suất của các biến cố sau:
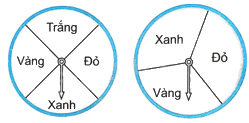
a) E: “Người chơi đạt giải nhất”;
b) F: “Người chơi đạt giải nhì”;
c) G: “Người chơi đạt giải ba”.
Phương pháp giải - Xem chi tiết
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết
Kí hiệu T, Đ, X, V lần lượt là các màu trắng, đỏ, xanh, vàng.
Ta có không gian mẫu: \(\Omega = \) {TĐ; TX; TV; ĐĐ; ĐX; ĐV; XĐ; XX; XV; VĐ; VX; VV}. Có 12 kết quả có thể là đồng khả năng.
a) Có 1 kết quả thuận lợi cho biến cố E là ĐĐ.
Do đó, \(P\left( E \right) = \frac{1}{{12}}\).
b) Có 3 kết quả thuận lợi cho biến cố F là ĐĐ, VV, XX.
Do đó, \(P\left( F \right) = \frac{3}{{12}} = \frac{1}{4}\).
c) Có 5 kết quả thuận lợi cho biến cố G là TĐ; ĐX; ĐV; XĐ; VĐ.
Do đó, \(P\left( G \right) = \frac{5}{{12}}\).
Trước khi đi vào giải chi tiết bài 8.14, chúng ta cùng ôn lại một số kiến thức cơ bản về hàm số bậc nhất và hàm số bậc hai. Hàm số bậc nhất có dạng y = ax + b (a ≠ 0), trong đó a là hệ số góc và b là tung độ gốc. Hàm số bậc hai có dạng y = ax² + bx + c (a ≠ 0), trong đó a, b, c là các hệ số. Việc hiểu rõ các tính chất của hàm số, đặc biệt là cách xác định hệ số và vẽ đồ thị hàm số, là rất quan trọng để giải quyết các bài toán liên quan.
Đề bài 8.14 thường yêu cầu học sinh xác định hàm số dựa trên các thông tin cho trước, hoặc tìm các tham số của hàm số để thỏa mãn một điều kiện nào đó. Để giải bài tập này, cần đọc kỹ đề bài, xác định rõ các yếu tố đã biết và yếu tố cần tìm. Sau đó, sử dụng các công thức và phương pháp đã học để thiết lập phương trình và giải phương trình đó.
(Phần này sẽ chứa lời giải chi tiết cho bài 8.14, bao gồm các bước giải, giải thích rõ ràng và các ví dụ minh họa. Lời giải sẽ được trình bày một cách logic và dễ hiểu, giúp học sinh nắm vững phương pháp giải.)
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 8.14, chúng ta sẽ cùng xem xét một số ví dụ minh họa. Sau đó, chúng ta sẽ đưa ra một số bài tập tương tự để các em tự luyện tập và củng cố kiến thức.
Để giải nhanh các bài tập về hàm số, các em có thể áp dụng một số mẹo sau:
Bài 8.14 trang 48 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng, giúp các em học sinh củng cố kiến thức về hàm số. Để học tốt môn Toán 9, các em cần nắm vững lý thuyết, luyện tập thường xuyên và tìm hiểu các phương pháp giải bài tập hiệu quả. Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và các hướng dẫn trên, các em sẽ tự tin hơn khi giải các bài tập về hàm số.
| Công thức | Mô tả |
|---|---|
| y = ax + b | Hàm số bậc nhất |
| y = ax² + bx + c | Hàm số bậc hai |
| x = -b/2a | Hoành độ đỉnh của parabol |