Bài 8.9 trang 46 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hệ phương trình bậc nhất hai ẩn để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8.9 trang 46, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Bạn Bình gieo một đồng xu cân đối và bạn Thịnh gieo một con xúc xắc cân đối. Tính xác suất của các biến cố sau: a) E: “Đồng xu xuất hiện mặt sấp và số chấm xuất hiện trên con xúc xắc lớn hơn 3”; b) F: “Đồng xu xuất hiện mặt ngửa hoặc số chấm xuất hiện trên con xúc xắc lớn hơn 3”.
Đề bài
Bạn Bình gieo một đồng xu cân đối và bạn Thịnh gieo một con xúc xắc cân đối. Tính xác suất của các biến cố sau:
a) E: “Đồng xu xuất hiện mặt sấp và số chấm xuất hiện trên con xúc xắc lớn hơn 3”;
b) F: “Đồng xu xuất hiện mặt ngửa hoặc số chấm xuất hiện trên con xúc xắc lớn hơn 3”.
Phương pháp giải - Xem chi tiết
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết
Kết quả của phép thử là (a, b) trong đó a và b tương ứng là số chấm trên con xúc xắc và mặt đồng xu.
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng như sau:
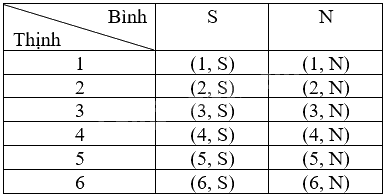
Mỗi ô ở bảng là một kết quả có thể. Có 12 kết quả có thể là đồng khả năng nên số phần tử của không gian mẫu là 12.
a) Có 3 kết quả thuận lợi cho biến cố E là: (5, S); (4, S); (6, S). Vậy\(P\left( E \right) = \frac{3}{{12}} = \frac{1}{4}\).
b) Có 9 kết quả thuận lợi cho biến cố F là: (1, N); (2, N); (3, N); (4, N); (5, N); (6, N); (5, S); (4, S); (6, S). Vậy \(P\left( F \right) = \frac{9}{{12}} = \frac{3}{4}\).
Bài 8.9 sách bài tập Toán 9 - Kết nối tri thức tập 2 yêu cầu giải một bài toán thực tế liên quan đến việc tìm hai số khi biết tổng và hiệu của chúng. Bài toán thường được trình bày dưới dạng một tình huống cụ thể, đòi hỏi học sinh phải chuyển đổi thông tin từ tình huống đó thành một hệ phương trình bậc nhất hai ẩn để giải.
Trước khi bắt đầu giải bài toán, điều quan trọng là phải đọc kỹ đề bài, hiểu rõ yêu cầu và xác định các đại lượng cần tìm. Sau đó, ta đặt ẩn số cho các đại lượng này. Ví dụ, nếu bài toán yêu cầu tìm hai số x và y, ta có thể đặt:
Dựa vào các thông tin được cung cấp trong đề bài, ta lập hệ phương trình bậc nhất hai ẩn. Hệ phương trình này sẽ mô tả mối quan hệ giữa các đại lượng đã đặt ẩn số. Ví dụ, nếu đề bài cho biết tổng của hai số là 10 và hiệu của chúng là 2, ta có hệ phương trình:
| x | y | = | |
|---|---|---|---|
| Phương trình 1 | 1 | 1 | 10 |
| Phương trình 2 | 1 | -1 | 2 |
Có nhiều phương pháp để giải hệ phương trình bậc nhất hai ẩn, bao gồm:
Trong ví dụ trên, ta có thể sử dụng phương pháp cộng đại số để giải hệ phương trình:
Cộng hai phương trình lại, ta được:
2x = 12
Suy ra x = 6
Thay x = 6 vào phương trình 1, ta được:
6 + y = 10
Suy ra y = 4
Sau khi tìm được giá trị của các ẩn, ta cần kiểm tra lại kết quả bằng cách thay các giá trị này vào các phương trình ban đầu để đảm bảo rằng chúng thỏa mãn các phương trình đó. Trong ví dụ trên, ta có:
6 + 4 = 10 (đúng)
6 - 4 = 2 (đúng)
Bài toán giải hệ phương trình bậc nhất hai ẩn có nhiều ứng dụng trong thực tế, chẳng hạn như:
Ngoài bài 8.9, sách bài tập Toán 9 - Kết nối tri thức tập 2 còn có nhiều bài tập tương tự về giải hệ phương trình bậc nhất hai ẩn. Để nắm vững kiến thức này, các em học sinh nên luyện tập thêm nhiều bài tập khác nhau.
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải bài 8.9 trang 46 sách bài tập Toán 9 - Kết nối tri thức tập 2 và các bài tập tương tự.