Bài 5.2 trang 56 sách bài tập Toán 9 Kết nối tri thức tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải phương trình bậc hai. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để tìm ra nghiệm của phương trình.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
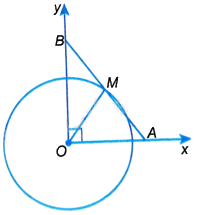
Cho đường tròn (O) có bán kính bằng 2,5cm và hai tia Ox, Oy vuông góc với nhau tại O. Trên tia Ox lấy điểm A sao cho (OA = 3cm); trên tia Oy lấy điểm B sao cho (OB = 4cm). Gọi M là trung điểm của đoạn AB. Chứng minh rằng điểm M nằm trên đường tròn (O).
Đề bài
Cho đường tròn (O) có bán kính bằng 2,5cm và hai tia Ox, Oy vuông góc với nhau tại O. Trên tia Ox lấy điểm A sao cho \(OA = 3cm\); trên tia Oy lấy điểm B sao cho \(OB = 4cm\). Gọi M là trung điểm của đoạn AB. Chứng minh rằng điểm M nằm trên đường tròn (O).
Phương pháp giải - Xem chi tiết
+ Áp dụng định lí Pythagore vào tam giác AOB vuông tại O tính được AB.
+ Vì OM là đường trung tuyến của tam giác AOB vuông tại O nên: \(OM = \frac{1}{2}AB\), tính được OM, suy ra M nằm trên đường tròn (O).
Lời giải chi tiết
Áp dụng định lí Pythagore vào tam giác AOB vuông tại O ta có: \(A{B^2} = A{O^2} + O{B^2} = {3^2} + {4^2} = 25\) nên \(AB = 5cm\).
Vì OM là đường trung tuyến của tam giác AOB vuông tại O nên: \(OM = \frac{1}{2}AB = 2,5cm\).
Do đó, M nằm trên đường tròn (O).
Bài 5.2 trang 56 sách bài tập Toán 9 Kết nối tri thức tập 1 yêu cầu giải phương trình bậc hai. Để giải bài tập này, chúng ta cần nắm vững các phương pháp giải phương trình bậc hai đã học, bao gồm:
Bài tập 5.2 thường bao gồm các phương trình bậc hai với các hệ số a, b, c khác nhau. Việc xác định đúng hệ số a, b, c là bước quan trọng để áp dụng đúng công thức nghiệm hoặc phương pháp giải phù hợp.
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể:
Bước 1: Xác định hệ số
a = 2, b = -5, c = 2
Bước 2: Tính delta (Δ)
Δ = b2 - 4ac = (-5)2 - 4 * 2 * 2 = 25 - 16 = 9
Bước 3: Tính nghiệm
Vì Δ > 0, phương trình có hai nghiệm phân biệt:
x1 = (-b + √Δ) / 2a = (5 + √9) / (2 * 2) = (5 + 3) / 4 = 2
x2 = (-b - √Δ) / 2a = (5 - √9) / (2 * 2) = (5 - 3) / 4 = 0.5
Kết luận: Phương trình 2x2 - 5x + 2 = 0 có hai nghiệm là x1 = 2 và x2 = 0.5
Ngoài bài tập 5.2, sách bài tập Toán 9 Kết nối tri thức tập 1 còn nhiều bài tập tương tự khác. Để giải các bài tập này, các em cần:
Trong một số trường hợp, có thể sử dụng các mẹo sau để giải nhanh phương trình bậc hai:
Để học toán 9 hiệu quả hơn, các em có thể tham khảo thêm các tài liệu sau:
Bài 5.2 trang 56 sách bài tập Toán 9 Kết nối tri thức tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải phương trình bậc hai. Hy vọng với hướng dẫn chi tiết và các mẹo giải nhanh trên đây, các em học sinh sẽ tự tin giải bài tập này và đạt kết quả tốt trong môn Toán.