Bài 9.42 trang 60 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học Toán 9. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.42 trang 60, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Một phép quay thuận chiều ({120^o}) tâm O biến điểm A thành điểm B, biến điểm B thành điểm C. Chứng tỏ rằng tam giác ABC là tam giác đều nội tiếp một đường tròn tâm O.
Đề bài
Một phép quay thuận chiều \({120^o}\) tâm O biến điểm A thành điểm B, biến điểm B thành điểm C. Chứng tỏ rằng tam giác ABC là tam giác đều nội tiếp một đường tròn tâm O.
Phương pháp giải - Xem chi tiết
+ Tính được các cung nhỏ AB, BC có số đo bằng \({120^o}\).
+ Tính được \(\widehat {ACB} = \frac{1}{2}\)sđ$\overset\frown{AB}={{60}^{o}}$, \(\widehat {BAC} = \frac{1}{2}\)sđ$\overset\frown{BC}={{60}^{o}}$, \(\widehat {ABC} = {180^o} - \widehat {ACB} - \widehat {BAC} = {60^o}\) nên tam giác ABC đều.
Lời giải chi tiết
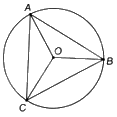
Ta có: \(OA = OB = OC\) nên tam giác ABC nội tiếp (O) và các cung nhỏ AB, BC có số đo bằng \({120^o}\).
Vì góc ACB và góc BAC là các góc nội tiếp đường tròn (O) lần lượt chắn các cung nhỏ AB, BC nên \(\widehat {ACB} = \frac{1}{2}\)sđ$\overset\frown{AB}$nhỏ\( = {60^o}\), \(\widehat {BAC} = \frac{1}{2}\)sđ$\overset\frown{BC}$ nhỏ \( = {60^o}\).
Tam giác ABC có: \(\widehat {ABC} = {180^o} - \widehat {ACB} - \widehat {BAC} = {60^o}\).
Tam giác ABC có: \(\widehat {ABC} = \widehat {ACB} = \widehat {CAB} = {60^o}\) nên tam giác ABC đều.
Bài 9.42 trang 60 sách bài tập Toán 9 - Kết nối tri thức tập 2 yêu cầu học sinh giải một bài toán liên quan đến hàm số bậc hai và ứng dụng của nó trong việc tìm giá trị lớn nhất hoặc nhỏ nhất của hàm số. Để giải bài toán này, chúng ta cần nắm vững các kiến thức sau:
Nội dung bài toán: (Giả sử bài toán cụ thể là tìm giá trị lớn nhất của hàm số y = -x2 + 4x - 1)
Lời giải:
Ngoài bài 9.42, sách bài tập Toán 9 - Kết nối tri thức tập 2 còn nhiều bài tập tương tự về hàm số bậc hai. Các bài tập này thường yêu cầu học sinh:
Để giải các bài tập này, học sinh cần nắm vững các kiến thức về hàm số bậc hai và luyện tập thường xuyên. Ngoài ra, việc sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm vẽ đồ thị cũng có thể giúp học sinh giải quyết bài toán một cách nhanh chóng và chính xác hơn.
Để học tốt môn Toán 9, các em học sinh cần:
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và những hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải bài 9.42 trang 60 sách bài tập Toán 9 - Kết nối tri thức tập 2 và đạt kết quả tốt trong môn Toán.
Bài tập: Tìm giá trị nhỏ nhất của hàm số y = x2 - 2x + 3.
Lời giải: