Bài 9.51 trang 62 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài toán quan trọng trong chương trình học. Bài toán này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.51 này, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho tam giác nhọn ABC có đường cao AH. Các điểm M và N lần lượt là hình chiếu vuông góc của H trên AB, AC. Chứng minh rằng (AM.AB = AN.AC).
Đề bài
Cho tam giác nhọn ABC có đường cao AH. Các điểm M và N lần lượt là hình chiếu vuông góc của H trên AB, AC. Chứng minh rằng \(AM.AB = AN.AC\).
Phương pháp giải - Xem chi tiết
+ Chứng minh tứ giác AMHN nội tiếp đường tròn đường kính AH, suy ra \(\widehat {AMN} = \widehat {AHN}\).
+ Ta có: \(\widehat {AMN} = \widehat {AHN} = {90^o} - \widehat {HAN} = \widehat {ACB}\).
+ Chứng minh $\Delta AMN\backsim \Delta ACB\left( g.g \right)$, suy ra \(AM.AB = AN.AC\).
Lời giải chi tiết
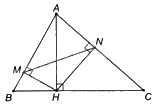
Vì \(\widehat {AMH} = \widehat {ANH} = {90^o}\) nên tam giác AMH vuông tại M và tam giác ANH vuông tại N.
Suy ra, hai tam giác AMH, ANH nội tiếp đường tròn đường kính AH.
Suy ra, tứ giác AMHN nội tiếp đường tròn đường kính AH.
Do đó, \(\widehat {AMN} = \widehat {AHN}\) (hai góc nội tiếp đường tròn đường kính AH cùng chắn cung AN).
Ta có: \(\widehat {AMN} = \widehat {AHN} = {90^o} - \widehat {HAN} = \widehat {ACB}\)
Tam giác AMN và tam giác ACB có:
\(\widehat {AMN} = \widehat {ACB}\) (cmt),
\(\widehat {MAN} = \widehat {CAB}\) (góc chung)
nên $\Delta AMN\backsim \Delta ACB\left( g.g \right)$.
Suy ra \(\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}\), suy ra \(AM.AB = AN.AC\).
Bài 9.51 yêu cầu chúng ta xét hàm số f(x) = x2 - 4x + 3 và thực hiện các yêu cầu sau:
Hàm số f(x) = x2 - 4x + 3 có dạng f(x) = ax2 + bx + c. Do đó:
Hoành độ đỉnh của parabol là x0 = -b / (2a) = -(-4) / (2 * 1) = 2.
Tung độ đỉnh của parabol là y0 = f(x0) = f(2) = 22 - 4 * 2 + 3 = 4 - 8 + 3 = -1.
Vậy đỉnh của parabol là I(2; -1).
Để vẽ đồ thị hàm số, ta cần xác định một số điểm thuộc đồ thị. Ngoài đỉnh I(2; -1), ta có thể tính thêm một vài điểm khác:
Vẽ parabol đi qua các điểm I(2; -1), A(0; 3), B(1; 0), C(3; 0), D(4; 3).
Tập xác định của hàm số là D = ℝ (tập hợp tất cả các số thực).
Vì a = 1 > 0 và đỉnh của parabol là I(2; -1), hàm số có tập giá trị là [-1; +∞).
Hàm số f(x) = x2 - 4x + 3 đồng biến trên khoảng (2; +∞) và nghịch biến trên khoảng (-∞; 2).
Qua bài giải chi tiết trên, chúng ta đã nắm vững cách giải bài 9.51 trang 62 sách bài tập Toán 9 - Kết nối tri thức tập 2. Hy vọng rằng, với lời giải này, các em học sinh sẽ tự tin hơn trong việc học tập và làm bài tập Toán 9.
Để củng cố kiến thức, các em có thể tham khảo thêm các bài toán tương tự trong sách bài tập Toán 9 - Kết nối tri thức tập 2, ví dụ như bài 9.52, 9.53,...
Khi giải các bài toán về hàm số bậc hai, cần nắm vững các kiến thức cơ bản về: