Bài 5.29 trang 71 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5.29, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Giả sử CD là một dây song song với đường kính AB của đường tròn (O) sao cho ABCD là một tứ giác lồi. Gọi E là trung điểm của đoạn CD. a) Chứng minh rằng A đối xứng với B và C đối xứng với D qua đường thẳng OE. b) Chứng minh rằng tứ giác ABCD là một hình thang cân. c) Biết rằng (AB = 12cm) và (widehat {COD} = {100^o}). Tính độ dài cung (nhỏ) AD và cung (lớn) ABC. d) Với giả thiết ở câu c, tính diện tích hình quạt tròn ứng với cung nhỏ BD.
Đề bài
Giả sử CD là một dây song song với đường kính AB của đường tròn (O) sao cho ABCD là một tứ giác lồi. Gọi E là trung điểm của đoạn CD.
a) Chứng minh rằng A đối xứng với B và C đối xứng với D qua đường thẳng OE.
b) Chứng minh rằng tứ giác ABCD là một hình thang cân.
c) Biết rằng \(AB = 12cm\) và \(\widehat {COD} = {100^o}\). Tính độ dài cung (nhỏ) AD và cung (lớn) ABC.
d) Với giả thiết ở câu c, tính diện tích hình quạt tròn ứng với cung nhỏ BD.
Phương pháp giải - Xem chi tiết
a) + Chứng minh tam giác COD cân tại O, suy ra OE là đường trung trực của đoạn thẳng CD. Vậy C và D đối xứng với nhau qua OE.
+ Chứng minh \(OE \bot CD\), mà CD//AB nên \(OE \bot AB\).
+ Chứng minh OE là đường trung trực của đoạn thẳng AB. Do đó, A và B đối xứng với nhau qua OE.
b) + Chứng minh OE là đường phân giác của góc COD, suy ra \(\widehat {{O_2}} = \widehat {{O_3}}\).
+ Ta có:
\(\widehat {AOC} = \widehat {AOE} + \widehat {EOC} \\= {90^o} + \widehat {{O_3}} = {90^o} + \widehat {{O_2}} = \widehat {DOE} + \widehat {EOB} = \widehat {DOB}\)
+ Chứng minh \(\Delta AOC = \Delta DOB\left( {c.g.c} \right)\), suy ra \(AC = BD\).
+ Tứ giác ABCD có: AB//CD nên ABCD là hình thang. Mà \(AC = BD\) nên ABCD là hình thang cân.
c) +Tính được bán kính của (O) bằng 6cm.
+ \(\widehat {{O_2}} = \widehat {{O_3}} = \frac{1}{2}\widehat {COD},\widehat {AOC} = \widehat {AOE} + \widehat {{O_2}}\), từ đó tính được sđ$\overset\frown{AD}$nhỏ \( = {140^o}\), suy ra độ dài cung nhỏ AD.
+ sđ$\overset\frown{AC}$lớn\( = {360^o} - \widehat {AOC}\) nên tính được độ dài cung lớn AC.
d) + Tính góc BOD nên tính được cung nhỏ BD nên sđ$\overset\frown{BD}$nhỏ từ đó tính được diện tích hình quạt tròn ứng với cung nhỏ BD.
Lời giải chi tiết
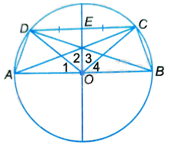
a) Vì \(OC = OD\) nên tam giác COD cân tại O. Do đó, OE là đường trung tuyến đồng thời là đường trung trực của tam giác COD hay OE là đường trung trực của đoạn thẳng CD.
Vậy C và D đối xứng với nhau qua OE.
Vì OE là đường trung trực của đoạn thẳng CD nên \(OE \bot CD\).
Mà CD//AB nên \(OE \bot AB\).
Mà O là trung điểm của AB do đó OE là đường trung trực của đoạn thẳng AB.
Do đó, A và B đối xứng với nhau qua OE.
b) Tam giác COD cân tại O nên OE là đường trung trực và là đường phân giác của góc COD, suy ra \(\widehat {{O_2}} = \widehat {{O_3}}\).
Ta có:
\(\widehat {AOC} = \widehat {AOE} + \widehat {EOC} \\= {90^o} + \widehat {{O_3}} = {90^o} + \widehat {{O_2}} = \widehat {DOE} + \widehat {EOB} = \widehat {DOB}\)
Tam giác AOC và tam giác DOB có: \(OA = OB = OC = OD\), \(\widehat {AOC} = \widehat {DOB}\) nên \(\Delta AOC = \Delta DOB\left( {c.g.c} \right)\)
Suy ra \(AC = BD\).
Tứ giác ABCD có: AB//CD nên ABCD là hình thang.
Mà \(AC = BD\) nên ABCD là hình thang cân.
c) Vì \(AB = 12cm\) nên bán kính của (O) bằng 6cm.
Lại có: \(\widehat {{O_2}} = \widehat {{O_3}} = \frac{1}{2}\widehat {COD} = {50^o},\)
\(\widehat {AOC} = \widehat {AOE} + \widehat {{O_2}} = {90^o} + {50^o} = {140^o}\).
Vì AOD là góc ở tâm chắn cung nhỏ AD nên sđ$\overset\frown{AD}$nhỏ\( = \widehat {AOD} = {90^o} - \widehat {{O_2}} = {40^o}\).
Độ dài cung nhỏ AD là:
\({l_{AD}} = \frac{{40}}{{180}}.\pi .6 = \frac{4}{3}\pi \left( {cm} \right)\)
Vì AOC là góc ở tâm chắn cung nhỏ AC nên sđ$\overset\frown{AC}$lớn\( = {360^o} - \widehat {AOC} = {220^o}\).
Độ dài cung lớn AC là:
\({l_{AC}} = \frac{{220}}{{180}}.\pi .6 = \frac{{22}}{3}\pi \left( {cm} \right)\)
d) \(\widehat {BOD} = \widehat {BOE} + \widehat {{O_2}} = {90^o} + {50^o} = {140^o}\).
Vì BOD là góc ở tâm chắn cung nhỏ BD nên sđ$\overset\frown{BD}$nhỏ\( = \widehat {BOD} = {140^o}\).
Diện tích hình quạt tròn ứng với cung nhỏ BD là:
\({S_q} = \frac{{140}}{{360}}.\pi {.6^2} = 14\pi \left( {c{m^2}} \right)\).
Bài 5.29 yêu cầu học sinh giải một bài toán liên quan đến việc xác định phương trình đường thẳng đi qua hai điểm cho trước. Cụ thể, bài toán thường cho hai điểm A(x1, y1) và B(x2, y2) và yêu cầu tìm phương trình đường thẳng AB.
Để giải bài toán này, chúng ta có thể sử dụng một trong các phương pháp sau:
Để giải bài 5.29 trang 71, chúng ta cần xác định chính xác tọa độ của hai điểm A và B. Sau đó, áp dụng một trong các phương pháp trên để tìm phương trình đường thẳng AB.
Ví dụ: Giả sử A(1, 2) và B(3, 4). Ta có thể sử dụng phương pháp tính hệ số góc:
Việc tìm phương trình đường thẳng có nhiều ứng dụng trong thực tế, chẳng hạn như:
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự sau:
Bài 5.29 trang 71 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tìm phương trình đường thẳng. Hy vọng với lời giải chi tiết và các lưu ý trên, các em học sinh sẽ tự tin hơn khi giải bài tập này.
| Công thức | Mô tả |
|---|---|
| m = (y2 - y1) / (x2 - x1) | Hệ số góc của đường thẳng AB |
| y = mx + b | Phương trình đường thẳng có hệ số góc m |
| (y - y1) / (x - x1) = (y2 - y1) / (x2 - x1) | Phương trình đường thẳng đi qua hai điểm A và B |