Bài 4.14 trang 46 sách bài tập Toán 9 Kết nối tri thức tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hệ phương trình bậc nhất hai ẩn để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.14 trang 46, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Tính tang, côtang của góc kề đáy của tam giác cân biết cạnh đáy dài 8cm, đường cao ứng với đáy dài 5cm.
Đề bài
Tính tang, côtang của góc kề đáy của tam giác cân biết cạnh đáy dài 8cm, đường cao ứng với đáy dài 5cm.
Phương pháp giải - Xem chi tiết
+ Giả sử tam giác ABC cân tại A có đáy \(BC = 8cm\). Kẻ đường cao AD của tam giác cân ABC nên \(AD = 5cm\).
+ Chứng minh AD là đường trung tuyến của tam giác ABC, từ đó tính được BD.
+ Tam giác ABD vuông tại D nên \(\tan B = \frac{{AD}}{{BD}};\cot B = \frac{{BD}}{{AD}}\).
Lời giải chi tiết
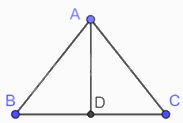
Giả sử tam giác ABC cân tại A có đáy \(BC = 8cm\). Kẻ đường cao AD của tam giác cân ABC nên \(AD = 5cm\).
Vì tam giác ABC cân tại A nên AD là đường cao đồng thời là đường trung tuyến.
Do đó, \(BD = \frac{{BC}}{2} = 4cm\).
Tam giác ABD vuông tại D nên \(\tan B = \frac{{AD}}{{BD}} = \frac{5}{4};\cot B = \frac{{BD}}{{AD}} = \frac{4}{5}\).
Bài 4.14 trang 46 sách bài tập Toán 9 Kết nối tri thức tập 1 yêu cầu giải bài toán về việc tìm số tiền mà mỗi người nhận được sau khi chia sẻ một khoản tiền. Để giải bài toán này, chúng ta cần thiết lập một hệ phương trình bậc nhất hai ẩn dựa trên các thông tin được cung cấp trong đề bài.
Đề bài cho biết: Một người có một số tiền, người đó chia cho con trai và con gái. Sau khi chia, người con trai nhận được nhiều hơn người con gái 200 nghìn đồng. Tổng số tiền mà hai người con nhận được là 2 triệu đồng. Chúng ta cần tìm số tiền mà mỗi người con nhận được.
Đặt:
Dựa vào các thông tin của đề bài, ta có thể thiết lập hệ phương trình sau:
| Phương trình | Giải thích |
|---|---|
| x - y = 200000 | Số tiền con trai nhận được nhiều hơn con gái 200 nghìn đồng |
| x + y = 2000000 | Tổng số tiền hai người con nhận được là 2 triệu đồng |
Chúng ta có thể giải hệ phương trình này bằng phương pháp cộng đại số:
(x - y) + (x + y) = 200000 + 2000000
2x = 2200000
x = 1100000
1100000 + y = 2000000
y = 900000
Vậy, người con trai nhận được 1.100.000 đồng và người con gái nhận được 900.000 đồng.
Để củng cố kiến thức về hệ phương trình bậc nhất hai ẩn, bạn có thể luyện tập thêm các bài tập tương tự trong sách bài tập Toán 9 Kết nối tri thức tập 1. Hãy chú ý phân tích đề bài, thiết lập hệ phương trình và giải hệ phương trình một cách cẩn thận.
Giaitoan.edu.vn là một website học toán online uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập Toán 9. Chúng tôi hy vọng rằng với những hướng dẫn trên, các em học sinh sẽ tự tin hơn trong việc giải bài tập Toán 9 và đạt kết quả tốt trong học tập.
Chúc các em học tốt!