Bài 10.12 trang 68 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 10.12 trang 68, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Một chiếc hộp hình lập phương có cạnh bằng 18cm đựng vừa khít một quả bóng hình cầu (H.10.4). Tính thể tích của quả bóng (coi độ dày của hộp không đáng kể).
Đề bài
Một chiếc hộp hình lập phương có cạnh bằng 18cm đựng vừa khít một quả bóng hình cầu (H.10.4). Tính thể tích của quả bóng (coi độ dày của hộp không đáng kể).
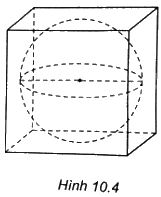
Phương pháp giải - Xem chi tiết
Thể tích hình cầu bán kính R là: \(V = \frac{4}{3}\pi {R^3}\).
Lời giải chi tiết
Bán kính của quả bóng là: \(R = 18:2 = 9\left( {cm} \right)\).
Thể tích của quả bóng là: \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.9^3} = 972\pi \left( {c{m^3}} \right)\).
Bài 10.12 trang 68 sách bài tập Toán 9 - Kết nối tri thức tập 2 yêu cầu chúng ta giải một bài toán liên quan đến ứng dụng của hàm số bậc nhất và hàm số bậc hai trong thực tế. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về:
Nội dung bài toán: (Giả sử bài toán có nội dung cụ thể về một tình huống thực tế, ví dụ: một vật thể chuyển động, một hình học, một bài toán kinh tế,...). Chúng ta sẽ phân tích bài toán này theo các bước sau:
Ví dụ minh họa: (Giả sử bài toán cụ thể là: Một vật được ném lên từ mặt đất với vận tốc ban đầu là 15 m/s. Hãy tìm thời gian để vật đạt độ cao tối đa và độ cao tối đa đó là bao nhiêu?).
Giải:
Gọi h(t) là độ cao của vật tại thời điểm t (giây). Ta có công thức:
h(t) = v0t - (1/2)gt2
Trong đó:
Vậy, h(t) = 15t - 4.9t2
Đây là một hàm số bậc hai có dạng h(t) = at2 + bt + c, với a = -4.9, b = 15, c = 0.
Đỉnh của parabol là điểm có hoành độ x = -b/(2a) = -15/(2*(-4.9)) ≈ 1.53 giây.
Độ cao tối đa là h(1.53) = 15*1.53 - 4.9*(1.53)2 ≈ 11.48 mét.
Kết luận: Vật đạt độ cao tối đa sau khoảng 1.53 giây và độ cao tối đa đó là khoảng 11.48 mét.
Lưu ý:
Các bài tập tương tự:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ hiểu rõ cách giải bài 10.12 trang 68 sách bài tập Toán 9 - Kết nối tri thức tập 2 và tự tin hơn trong việc học Toán 9. Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục tri thức!
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc nhất | Hàm số có dạng y = ax + b, với a ≠ 0. |
| Hàm số bậc hai | Hàm số có dạng y = ax2 + bx + c, với a ≠ 0. |