Bài 7.14 trang 31 sách bài tập Toán 9 Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và ứng dụng thực tế để giải quyết vấn đề.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.14 trang 31, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho biểu đồ hình quạt tròn sau: a) Giải thích các số liệu được biểu diễn trên biểu đồ. b) Lập bảng tần số tương đối cho dữ liệu được biểu diễn trên biểu đồ.
Đề bài
Cho biểu đồ hình quạt tròn sau:
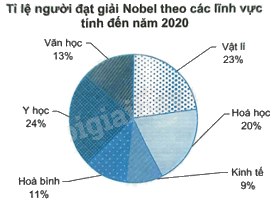
a) Giải thích các số liệu được biểu diễn trên biểu đồ.
b) Lập bảng tần số tương đối cho dữ liệu được biểu diễn trên biểu đồ.
Phương pháp giải - Xem chi tiết
a) Chỉ ra các lĩnh vực giải Nobel và ứng với tỉ lệ người đạt giải tính đến năm 2020.
b) Lập bảng tần số tương đối:
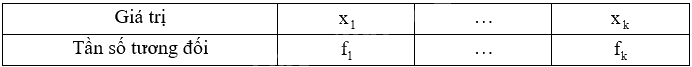
Trong đó, giá trị \({x_i}\) có tần số tương đối là \({f_i}\).
Lời giải chi tiết
a) Trong số những người đạt giải Nobel tính đến năm 2020, số người đạt giải Nobel về Vật lí, Hóa học, Kinh tế, Hòa bình, Y học, Văn học chiếm các tỉ lệ tương ứng là 23%, 20%, 9%, 11%, 24%, 13%.
b) Bảng tần số tương đối:

Bài 7.14 trang 31 sách bài tập Toán 9 Kết nối tri thức tập 2 thuộc chương Hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Phương pháp giải bài tập hàm số bậc nhất thường bao gồm các bước sau:
Đề bài: (Nội dung đề bài sẽ được chèn vào đây - ví dụ: Một người đi xe đạp với vận tốc 15km/h. Hỏi sau 2 giờ người đó đi được bao nhiêu km?)
Lời giải:
Gọi x là thời gian người đó đi xe đạp (giờ), y là quãng đường người đó đi được (km). Ta có hàm số biểu diễn mối quan hệ giữa thời gian và quãng đường là:
y = 15x
Khi x = 2 giờ, ta có:
y = 15 * 2 = 30 (km)
Vậy sau 2 giờ người đó đi được 30 km.
Ngoài bài 7.14, sách bài tập Toán 9 Kết nối tri thức tập 2 còn nhiều bài tập tương tự về hàm số bậc nhất. Các bài tập này thường yêu cầu học sinh:
Để giải các bài tập này, học sinh cần luyện tập thường xuyên và nắm vững các kiến thức cơ bản về hàm số bậc nhất.
Hàm số bậc nhất có rất nhiều ứng dụng trong thực tế, ví dụ:
Việc hiểu rõ và vận dụng hàm số bậc nhất vào các bài toán thực tế giúp học sinh rèn luyện tư duy logic và khả năng giải quyết vấn đề.
Để củng cố kiến thức về bài 7.14 và các bài tập tương tự, các em học sinh có thể tự giải các bài tập sau:
Bài 7.14 trang 31 sách bài tập Toán 9 Kết nối tri thức tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó. Hy vọng với lời giải chi tiết và các kiến thức bổ sung trên, các em học sinh sẽ tự tin hơn khi làm bài tập Toán 9.