Bài 5.8 trang 59 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để xác định hệ số góc và đường thẳng song song.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững phương pháp giải bài tập và tự tin hơn trong quá trình học tập.
Gọi H là trung điểm của dây AB không đi qua tâm của đường tròn (O). a) Chứng minh rằng (OH bot AB). b) Tính khoảng cách từ O đến AB, biết rằng (AB = 8cm) và bán kính của (O) bằng 5cm.
Đề bài
Gọi H là trung điểm của dây AB không đi qua tâm của đường tròn (O).
a) Chứng minh rằng \(OH \bot AB\).
b) Tính khoảng cách từ O đến AB, biết rằng \(AB = 8cm\) và bán kính của (O) bằng 5cm.
Phương pháp giải - Xem chi tiết
a) Chứng minh tam giác OAB cân tại O, suy ra OH là đường cao của tam giác ABO nên \(OH \bot AB\).
b) + Chỉ ra khoảng cách từ O đến AB là OH.
+ Áp dụng định lí Pythagore vào tam giác BOH vuông tại H tính được OH.
Lời giải chi tiết
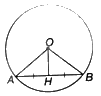
a) Tam giác ABO có: \(OA = OB\) (bán kính đường tròn (O)) nên tam giác ABO cân tại O. Do đó, OH là đường trung tuyến đồng thời là đường cao của tam giác ABO. Suy ra \(OH \bot AB\).
b) Vì \(OH \bot AB\) tại H nên khoảng cách từ O đến AB là OH.
Ta có: \(HB = \frac{{AB}}{2} = 4cm\)
Áp dụng định lí Pythagore vào tam giác BOH vuông tại H ta có: \(O{H^2} + H{B^2} = O{B^2}\)
\(OH = \sqrt {O{B^2} - H{B^2}} = \sqrt {{5^2} - {4^2}} = 3\left( {cm} \right)\)
Vậy khoảng cách từ O đến AB bằng 3cm.
Bài 5.8 yêu cầu chúng ta xét một tình huống thực tế liên quan đến việc tính toán quãng đường và thời gian di chuyển. Để giải bài toán này, chúng ta cần hiểu rõ về hàm số bậc nhất và cách xác định hệ số góc của đường thẳng.
Một người đi xe đạp từ A đến B với vận tốc 12km/h. Sau khi đi được 1 giờ, người đó tăng vận tốc lên 15km/h và đến B sau 30 phút nữa. Tính độ dài quãng đường AB.
Bài toán này có thể được giải bằng cách chia quãng đường AB thành hai đoạn: đoạn đường đi với vận tốc 12km/h và đoạn đường đi với vận tốc 15km/h. Thời gian đi trên mỗi đoạn đường là khác nhau, và chúng ta cần sử dụng công thức quãng đường = vận tốc × thời gian để tính toán.
Tổng độ dài quãng đường AB: 12km + 7.5km = 19.5km
Độ dài quãng đường AB là 19.5km.
Bài toán này có thể được giải bằng nhiều cách khác nhau, ví dụ như sử dụng phương trình bậc nhất một ẩn. Tuy nhiên, cách giải sử dụng hàm số bậc nhất giúp chúng ta hiểu rõ hơn về mối quan hệ giữa vận tốc, thời gian và quãng đường.
Một ô tô đi từ A đến B với vận tốc 60km/h. Sau khi đi được 2 giờ, ô tô giảm vận tốc xuống 40km/h và đến B sau 1 giờ nữa. Tính độ dài quãng đường AB.
Khi giải các bài toán liên quan đến vận tốc, thời gian và quãng đường, chúng ta cần chú ý đến đơn vị đo lường. Đảm bảo rằng tất cả các đơn vị đều tương đồng trước khi thực hiện các phép tính.
Giaitoan.edu.vn là một nền tảng học toán online uy tín, cung cấp đầy đủ các tài liệu học tập, bài giảng, bài tập và lời giải chi tiết cho các môn Toán từ lớp 6 đến lớp 12. Chúng tôi cam kết mang đến cho học sinh một môi trường học tập hiệu quả, giúp các em nắm vững kiến thức và đạt kết quả cao trong học tập.
Hãy truy cập giaitoan.edu.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích và bắt đầu hành trình chinh phục môn Toán!