Bài 5.34 trang 72 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5.34 trang 72, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài với nhau tại A, hai điểm (B in left( O right)) và (C in left( {O'} right)) sao cho B và C nằm cùng phía đối với đường thẳng OO’ và OB//O’C. a) Chứng minh góc BAC là góc vuông. b) Cho biết (R = 3cm), (R' = 1cm) và BC cắt OO’ tại D. Tính độ dài đoạn OD.
Đề bài
Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài với nhau tại A, hai điểm \(B \in \left( O \right)\) và \(C \in \left( {O'} \right)\) sao cho B và C nằm cùng phía đối với đường thẳng OO’ và OB//O’C.
a) Chứng minh góc BAC là góc vuông.
b) Cho biết \(R = 3cm\), \(R' = 1cm\) và BC cắt OO’ tại D. Tính độ dài đoạn OD.
Phương pháp giải - Xem chi tiết
a) + Chứng minh tam giác AOB cân tại O nên \(\widehat {{A_1}} = \widehat {{B_1}}\).
+ Tam giác AOB có:
\(\widehat {{A_1}} + \widehat {{O_1}} + \widehat {{B_1}} = 2\widehat {{A_1}} + \widehat {{O_1}} = {180^o}\) nên \(2\widehat {{A_1}} = {180^o} - \widehat {{O_1}}\).
+ Chứng minh tam giác AO’C cân tại O’. Do đó, \(\widehat {{A_2}} = \widehat {O'CA}\).
+ Tam giác AO’C có:
\(\widehat {{A_2}} + \widehat {O{'_1}} + \widehat {O'CA} = 2\widehat {{A_2}} + \widehat {O{'_1}} = {180^o}\) nên \(2\widehat {{A_2}} = {180^o} - \widehat {O{'_1}}\).
+ Do đó:
\(2\left( {\widehat {{A_1}} + \widehat {{A_2}}} \right) = {360^o} - \left( {\widehat {{O_1}} + \widehat {O{'_1}}} \right)\) (1)
Chứng minh
\(\widehat {{O_2}} = \widehat {O{'_1}}\), \(\widehat {{O_2}} + \widehat {{O_1}} = {180^o}\) nên \(\widehat {{O_1}} + \widehat {O{'_1}} = {180^o}\) (2)
Từ (1) và (2) ta có:
\(2\left( {\widehat {{A_1}} + \widehat {{A_2}}} \right) = {360^o} - {180^o} = {180^o}\) nên \(\widehat {BAC} = {90^o}\).
b) + Ta có: \(OA = OB = R = 3cm,O'A = O'C = R' = 1cm\).
+ Chứng minh \(\frac{{DO}}{{DO'}} = \frac{{OB}}{{O'C}} = \frac{3}{1}\)
+ \(DO' = DO - OO' = DO - \left( {OA + O'A} \right)\) \( = DO - \left( {3 + 1} \right) = DO - 4\) (4)
+ Do đó, \(\frac{{DO}}{{DO - 4}} = \frac{3}{1}\), từ đó tính được DO.
Lời giải chi tiết
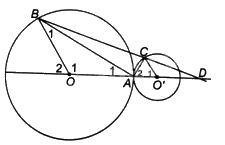
a) Vì \(OA = OB\) (bán kính của (O)) nên tam giác AOB cân tại O. Do đó, \(\widehat {{A_1}} = \widehat {{B_1}}\).
Tam giác AOB có:
\(\widehat {{A_1}} + \widehat {{O_1}} + \widehat {{B_1}} = 2\widehat {{A_1}} + \widehat {{O_1}} = {180^o}\) nên \(2\widehat {{A_1}} = {180^o} - \widehat {{O_1}}\).
Vì \(O'A = O'C\) (bán kính của (O’)) nên tam giác AO’C cân tại O’. Do đó, \(\widehat {{A_2}} = \widehat {O'CA}\).
Tam giác AO’C có:
\(\widehat {{A_2}} + \widehat {O{'_1}} + \widehat {O'CA} = 2\widehat {{A_2}} + \widehat {O{'_1}} = {180^o}\) nên \(2\widehat {{A_2}} = {180^o} - \widehat {O{'_1}}\).
Do đó:
\(2\left( {\widehat {{A_1}} + \widehat {{A_2}}} \right) = {360^o} - \left( {\widehat {{O_1}} + \widehat {O{'_1}}} \right)\) (1)
Vì OB//O’C nên \(\widehat {{O_2}} = \widehat {O{'_1}}\) (hai góc đồng vị).
Lại có: \(\widehat {{O_2}} + \widehat {{O_1}} = {180^o}\) nên \(\widehat {{O_1}} + \widehat {O{'_1}} = {180^o}\) (2).
Từ (1) và (2) ta có:
\(2\left( {\widehat {{A_1}} + \widehat {{A_2}}} \right) = {360^o} - {180^o} = {180^o}\) nên \(\widehat {{A_1}} + \widehat {{A_2}} = {90^o}\), suy ra \(\widehat {BAC} = {90^o}\).
b) Ta có: \(OA = OB = R = 3cm,O'A = O'C = R' = 1cm\).
Tam giác DOB có O’C//OB nên
\(\frac{{DO}}{{DO'}} = \frac{{OB}}{{O'C}} = \frac{3}{1}\) (3)
Lại có:
\(DO' = DO - OO' = DO - \left( {OA + O'A} \right) \\= DO - \left( {3 + 1} \right) = DO - 4 \;(4)\)
Từ (3) và (4) ta có:
\(\frac{{DO}}{{DO - 4}} = \frac{3}{1}\), suy ra \(DO = 3\left( {DO - 4} \right)\), hay \(2DO = 12\), suy ra \(DO = 6cm\).
Bài 5.34 trang 72 sách bài tập Toán 9 - Kết nối tri thức tập 1 thuộc chương Hàm số bậc nhất và hàm số bậc hai. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Đề bài: (Đề bài cụ thể của bài 5.34 sẽ được trình bày ở đây. Ví dụ: Cho hàm số y = 2x + 3. Tìm giá trị của y khi x = -1.)
Lời giải:
Để giúp các em hiểu rõ hơn về cách giải bài 5.34, chúng ta cùng xem xét một số ví dụ minh họa và bài tập tương tự:
Ví dụ 1: (Đề bài ví dụ 1 và lời giải chi tiết)
Ví dụ 2: (Đề bài ví dụ 2 và lời giải chi tiết)
Ngoài bài 5.34, các em có thể luyện tập thêm các bài tập khác trong sách bài tập Toán 9 - Kết nối tri thức tập 1 để củng cố kiến thức và kỹ năng giải toán. Các em cũng có thể tìm kiếm các tài liệu tham khảo khác trên mạng internet hoặc tại các thư viện để mở rộng kiến thức về hàm số.
Bài 5.34 trang 72 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng giúp các em củng cố kiến thức về hàm số. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em sẽ tự tin hơn khi giải các bài tập tương tự. Chúc các em học tốt!
| Hàm số | Đặc điểm |
|---|---|
| y = ax + b | Hàm số bậc nhất, đồ thị là đường thẳng. |
| y = ax2 + bx + c | Hàm số bậc hai, đồ thị là parabol. |