Bài 6.6 trang 7 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hệ phương trình bậc nhất hai ẩn để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6.6 trang 7, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Trên cùng một mặt phẳng tọa độ Oxy, vẽ parabol (P): (y = - {x^2}) và đường thẳng (d): (y = x - 2). Dùng đồ thị xác định tọa độ các giao điểm của hai đường này.
Đề bài
Trên cùng một mặt phẳng tọa độ Oxy, vẽ parabol (P): \(y = - {x^2}\) và đường thẳng (d): \(y = x - 2\). Dùng đồ thị xác định tọa độ các giao điểm của hai đường này.
Phương pháp giải - Xem chi tiết
Cách vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\):
+ Lập bảng ghi một số cặp giá trị tương ứng của x và y.
+ Trong mặt phẳng tọa độ Oxy, biểu diễn các cặp điểm (x; y) trong bảng giá trị trên và nối chúng lại để được một đường cong là đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\).
Cách vẽ đồ thị hàm số \(y = ax + b\): Biểu diễn tọa độ hai điểm thuộc đồ thị hàm số \(y = ax + b\). Nối hai điểm đó với nhau ta được đồ thị của hàm số \(y = ax + b\).
Lời giải chi tiết
Lập bảng một số giá trị tương ứng giữa x và y:

Đường thẳng d đi qua hai điểm (0; -2) và (2; 0).
Đồ thị của hai hàm số \(y = - {x^2}\) và \(y = x - 2\).
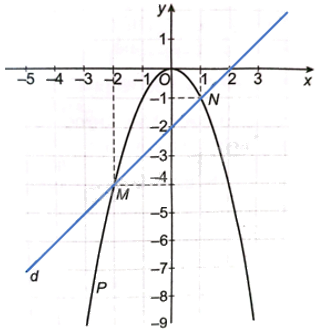
Từ hình vẽ ta có, giao điểm của hai đường này là M(-2; -4) và N(1; -1).
Bài 6.6 trang 7 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài toán ứng dụng thực tế, giúp học sinh củng cố kiến thức về hệ phương trình bậc nhất hai ẩn. Dưới đây là đề bài và lời giải chi tiết:
Đề bài:
Một người đi xe máy từ A đến B với vận tốc 40km/h. Nếu người đó tăng vận tốc thêm 5km/h thì sẽ đến B sớm hơn 18 phút. Tính quãng đường AB.
Lời giải:
Từ (1) và (2) ta có hệ phương trình:
| x | t | |
|---|---|---|
| (1) | x = 40t | |
| (2) | x = 45(t - 0.3) |
Thay (1) vào (2) ta được:
40t = 45(t - 0.3)
40t = 45t - 13.5
5t = 13.5
t = 2.7 (giờ)
Thay t = 2.7 vào (1) ta được:
x = 40 * 2.7 = 108 (km)
Vậy quãng đường AB là 108km.
Để giải bài toán này, học sinh cần nắm vững các kiến thức sau:
Ngoài ra, học sinh có thể tham khảo các bài tập tương tự để rèn luyện kỹ năng giải hệ phương trình và ứng dụng vào các bài toán thực tế.
Khi giải bài tập về hệ phương trình, học sinh cần chú ý:
Giaitoan.edu.vn hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về bài 6.6 trang 7 sách bài tập Toán 9 - Kết nối tri thức tập 2 và tự tin hơn trong quá trình học tập.