Bài 9.32 trang 57 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài toán quan trọng trong chương trình học. Bài toán này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các vấn đề thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.32, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho tam giác nhọn ABC có các đường cao BE, CF. Một đường tròn (O) đi qua hai điểm E, F và cắt các tia đối của hai tia BF, CE lần lượt tại X và Y. Chứng minh rằng XY song song với BC.
Đề bài
Cho tam giác nhọn ABC có các đường cao BE, CF. Một đường tròn (O) đi qua hai điểm E, F và cắt các tia đối của hai tia BF, CE lần lượt tại X và Y. Chứng minh rằng XY song song với BC.
Phương pháp giải - Xem chi tiết
+ Chứng minh bốn điểm B, E, F, C cùng nằm trên đường tròn có tâm là trung điểm của BC, đường kính BC, suy ra tứ giác BFEC là tứ giác nội tiếp.
+ Chứng minh \(\widehat {FBC} = {180^o} - \widehat {FEC} = {180^o} - \widehat {FEY} = \widehat {FXY}\), suy ra XY song song với BC.
Lời giải chi tiết
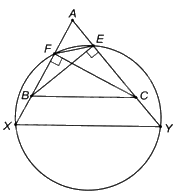
Vì các tam giác vuông BEC, BFC có chung cạnh huyền BC nên bốn điểm B, E, F, C cùng nằm trên đường tròn có tâm là trung điểm của BC và bán kính \(\frac{{BC}}{2}\). Do đó, tứ giác BFEC là tứ giác nội tiếp.
Vì tổng các góc đối nhau của các tứ giác nội tiếp BFEC và XFEY bằng 180 độ nên:
\(\widehat {FBC} = {180^o} - \widehat {FEC} = {180^o} - \widehat {FEY} = \widehat {FXY}\)
Mà hai góc này ở vị trí đồng vị nên XY song song với BC.
Bài 9.32 trang 57 sách bài tập Toán 9 - Kết nối tri thức tập 2 thuộc chương Hàm số bậc nhất và hàm số bậc hai. Bài toán này thường yêu cầu học sinh xác định hàm số, tìm điểm thuộc đồ thị hàm số, hoặc giải các bài toán liên quan đến ứng dụng của hàm số trong thực tế.
(Nội dung đề bài sẽ được chèn vào đây. Ví dụ: Cho hàm số y = 2x + 3. Tìm tọa độ giao điểm của đồ thị hàm số với đường thẳng y = -x + 6)
Để giải bài 9.32, học sinh cần nắm vững các kiến thức sau:
(Lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải, giải thích rõ ràng và dễ hiểu. Ví dụ: Để tìm tọa độ giao điểm của hai đường thẳng y = 2x + 3 và y = -x + 6, ta giải hệ phương trình sau:)
Thay phương trình (2) vào phương trình (1), ta được: 2x + 3 = -x + 6. Giải phương trình này, ta tìm được x = 1. Thay x = 1 vào phương trình (1), ta được y = 5. Vậy tọa độ giao điểm của hai đường thẳng là (1; 5).
Ngoài bài 9.32, học sinh có thể gặp các dạng bài tập tương tự như:
Để giải tốt các bài tập về hàm số bậc nhất và hàm số bậc hai, học sinh nên:
Bài 9.32 trang 57 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài toán quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và hàm số bậc hai. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!
| STT | Nội dung |
|---|---|
| 1 | Định nghĩa hàm số bậc nhất |
| 2 | Định nghĩa hàm số bậc hai |
| 3 | Cách vẽ đồ thị hàm số |
| Nguồn: Giaitoan.edu.vn | |