Bài 4.31 trang 51 sách bài tập toán 9 thuộc chương trình Kết nối tri thức tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức về cách xác định hệ số góc, đường thẳng song song và các ứng dụng của hàm số bậc nhất.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.31 trang 51 sách bài tập toán 9 - Kết nối tri thức tập 1, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
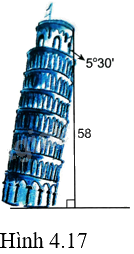
Chiều cao từ mặt đất đến đỉnh tháp Pisa ở Italia là 58m, tháp nghiêng góc ({5^o}30') đối với phương thẳng đứng (H.4.17). Khi Mặt Trời chiếu vuông góc với mặt đất thì bóng của tháp dài bao nhiêu decimét?
Đề bài
Chiều cao từ mặt đất đến đỉnh tháp Pisa ở Italia là 58m, tháp nghiêng góc \({5^o}30'\) đối với phương thẳng đứng (H.4.17). Khi Mặt Trời chiếu vuông góc với mặt đất thì bóng của tháp dài bao nhiêu decimét?
Phương pháp giải - Xem chi tiết
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tan góc đối.
Lời giải chi tiết
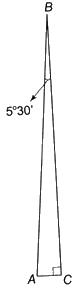
Gọi A là chân đỉnh tháp, B là đỉnh tháp, C là bóng chiếu thẳng đứng của đỉnh tháp thì tam giác ABC vuông tại C, \(BC = 58m,\widehat B = {5^o}30'\).
Khi đó, AC là bóng của tháp.
Tam giác ABC vuông tại A nên \(AC = BC.\tan B = 58.\tan {5^o}30' \approx 5,58m \approx 56dm.\)
Bài 4.31 trang 51 sách bài tập toán 9 - Kết nối tri thức tập 1 yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc xác định phương trình đường thẳng. Để giải bài toán này, chúng ta cần nắm vững các kiến thức sau:
Trước khi bắt đầu giải bài, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, đề bài sẽ cung cấp một số thông tin về đường thẳng, chẳng hạn như tọa độ của hai điểm thuộc đường thẳng, hệ số góc hoặc tung độ gốc. Dựa vào các thông tin này, chúng ta cần xác định phương trình đường thẳng cần tìm.
Có nhiều phương pháp để giải bài toán tìm phương trình đường thẳng, tùy thuộc vào thông tin được cung cấp trong đề bài. Một số phương pháp phổ biến bao gồm:
(Ở đây sẽ là lời giải chi tiết của bài toán 4.31, bao gồm các bước giải, giải thích rõ ràng và kết quả cuối cùng. Ví dụ:)
Bài 4.31: Cho hai điểm A(1; 2) và B(3; 6). Hãy tìm phương trình đường thẳng đi qua hai điểm A và B.
Giải:
1. Tính hệ số góc:
Hệ số góc của đường thẳng AB là: m = (yB - yA) / (xB - xA) = (6 - 2) / (3 - 1) = 4 / 2 = 2
2. Viết phương trình đường thẳng:
Phương trình đường thẳng AB có dạng: y = mx + b
Thay tọa độ điểm A(1; 2) và hệ số góc m = 2 vào phương trình, ta được:
2 = 2 * 1 + b => b = 0
Vậy phương trình đường thẳng AB là: y = 2x
3. Kết luận:
Phương trình đường thẳng đi qua hai điểm A(1; 2) và B(3; 6) là y = 2x.
Để nắm vững kiến thức về hàm số bậc nhất và phương trình đường thẳng, các em học sinh nên luyện tập thêm các bài tập tương tự. Giaitoan.edu.vn cung cấp nhiều bài tập khác với các mức độ khó khác nhau, giúp các em rèn luyện kỹ năng và tự tin hơn trong quá trình học tập.
Bài 4.31 trang 51 sách bài tập toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và phương trình đường thẳng. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể của Giaitoan.edu.vn, các em học sinh sẽ hiểu rõ phương pháp giải và tự tin làm bài tập.
Hãy tiếp tục luyện tập và khám phá thêm nhiều bài toán thú vị khác trên Giaitoan.edu.vn để nâng cao kiến thức và kỹ năng toán học của mình!