Bài 5.23 trang 68 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5.23 trang 68, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Vẽ hình và chứng minh phần b của Ví dụ 2. Cho đường tròn (O) và dây AB không là đường kính của (O). a) Gọi O' là một điểm tùy ý nằm giữa O và A. Đường thẳng đi qua O' và song song với OB cắt AB tại C. Hãy xác định vị trí tương đối của (O) và (O'; O'C). b) Vị trí tương đối của (O) và (O'; O'C) sẽ như thế nào nếu O' thẳng hàng với O và A, nhưng nằm ngoài đoạn OA?
Đề bài
Vẽ hình và chứng minh phần b của Ví dụ 2.
Ví dụ 2: Cho đường tròn (O) và dây AB không là đường kính của (O).a) Gọi O' là một điểm tùy ý nằm giữa O và A. Đường thẳng đi qua O' và song song với OB cắt AB tại C. Hãy xác định vị trí tương đối của (O) và (O'; O'C).b) Vị trí tương đối của (O) và (O'; O'C) sẽ như thế nào nếu O' thẳng hàng với O và A, nhưng nằm ngoài đoạn OA?
Phương pháp giải - Xem chi tiết
- Trường hợp 1: O và O’ nằm cùng phía với A (O nằm giữa O’ và A).
+ Chứng minh $\Delta O'AC\backsim \Delta OAB$.
+ Chứng minh tam giác OAB cân tại O, suy ra tam giác O’AC cân tại O’ và \(O'C = O'A\).
+ \(OO' = O'A - OA = O'C - OA\). Do đó, đường tròn (O’; O’C) tiếp xúc trong với đường tròn (O; OA).
- Trường hợp 2: O và O’ nằm khác phía với A (A nằm giữa O’ và O).
+ Chứng minh $\Delta O'AC\backsim \Delta OAB$.
+ Chứng minh tam giác OAB cân tại O. Do đó, tam giác O’AC cân tại O’ và \(O'C = O'A\).
+ \(OO' = O'A + OA = O'C + OA\). Do đó, đường tròn (O’; O’C) tiếp xúc ngoài với đường tròn (O; OA).
Lời giải chi tiết
Trường hợp 1: O và O’ nằm cùng phía với A (O nằm giữa O’ và A).
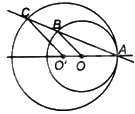
Vì CO’//OB nên $\Delta O'AC\backsim \Delta OAB$.
Vì OA=OB nên tam giác OAB cân tại O. Do đó, tam giác O’AC cân tại O’ và \(O'C = O'A\).
Lại có: \(OO' = O'A - OA = O'C - OA\). Do đó, đường tròn (O’; O’C) tiếp xúc trong với đường tròn (O; OA).
Trường hợp 2: O và O’ nằm khác phía với A (A nằm giữa O’ và O).
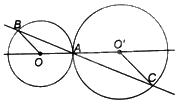
Vì CO’//OB nên $\Delta O'AC\backsim \Delta OAB$.
Vì OA=OB nên tam giác OAB cân tại O. Do đó, tam giác O’AC cân tại O’ và \(O'C = O'A\).
Lại có: \(OO' = O'A + OA = O'C + OA\). Do đó, đường tròn (O’; O’C) tiếp xúc ngoài với đường tròn (O; OA).
Bài 5.23 thuộc chương trình Toán 9, tập trung vào việc ứng dụng kiến thức về hàm số bậc nhất và hàm số bậc hai vào giải quyết các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản sau:
Đề bài: (Giả sử đề bài là một bài toán cụ thể về ứng dụng hàm số, ví dụ: Một người nông dân có một mảnh đất hình chữ nhật, chiều dài hơn chiều rộng 5m. Nếu tăng chiều rộng thêm 2m và giảm chiều dài đi 3m thì diện tích mảnh đất giảm đi 10m2. Tính chiều dài và chiều rộng ban đầu của mảnh đất.)
Giải:
Ngoài bài 5.23, còn rất nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về hàm số để giải quyết các vấn đề thực tế. Một số dạng bài tập thường gặp:
Để giải quyết các bài tập này, học sinh cần:
Để củng cố kiến thức và kỹ năng giải bài tập về hàm số, học sinh có thể tham khảo thêm các bài tập sau:
Bài 5.23 trang 68 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về hàm số vào giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán.