Bài 8.10 trang 46 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hệ phương trình bậc nhất hai ẩn để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8.10 trang 46, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Hai túi I và II chứa các viên bi có cùng kích thước. Túi I chứa 4 viên bi được ghi các số 1, 2, 3, 4. Túi II chứa 5 viên bi được ghi các số 1, 2, 3, 4, 5. Bạn Mai lấy ngẫu nhiên một viên bi từ túi I và bạn Tuấn lấy ngẫu nhiên một viên Bi từ túi II. Tính xác suất của các biến cố sau: a) A: “Hai số ghi trên hai viên bi khác nhau”; b) B: “Hai số ghi trên hai viên bi chênh nhau 1 đơn vị”; c) C: “Hai số ghi trên hai viên bi chênh nhau 3 đơn vị”.
Đề bài
Hai túi I và II chứa các viên bi có cùng kích thước. Túi I chứa 4 viên bi được ghi các số 1, 2, 3, 4. Túi II chứa 5 viên bi được ghi các số 1, 2, 3, 4, 5. Bạn Mai lấy ngẫu nhiên một viên bi từ túi I và bạn Tuấn lấy ngẫu nhiên một viên Bi từ túi II. Tính xác suất của các biến cố sau:
a) A: “Hai số ghi trên hai viên bi khác nhau”;
b) B: “Hai số ghi trên hai viên bi chênh nhau 1 đơn vị”;
c) C: “Hai số ghi trên hai viên bi chênh nhau 3 đơn vị”.
Phương pháp giải - Xem chi tiết
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết
Kết quả của phép thử là một cặp số (a, b) trong đó a và b tương ứng là số ghi trên viên bi túi II và túi I.
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng như sau:
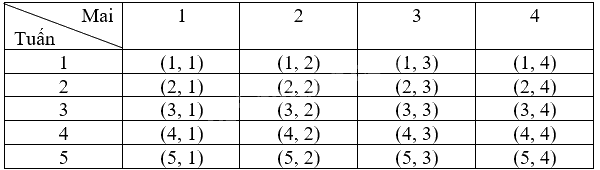
Có 20 kết quả có thể là đồng khả năng nên \(n\left( \Omega \right) = 20\).
a) Bỏ đi 4 ô (1, 1); (2, 2); (3, 3); (4, 4) ta có: \(20 - 4 = 16\) kết quả thuận lợi của biến cố A. Do đó, \(P\left( A \right) = \frac{{16}}{{20}} = \frac{4}{5}\).
b) Có 7 kết quả thuận lợi của biến cố B: (1, 2); (2, 1); (3, 2); (2, 3); (4, 3); (3, 4); (5, 4). Do đó, \(P\left( B \right) = \frac{7}{{20}}\).
c) Có 3 kết quả thuận lợi của biến cố C: (1, 4); (4, 1); (5, 2). Do đó, \(P\left( C \right) = \frac{3}{{20}}\).
Bài 8.10 yêu cầu giải bài toán về việc tìm số tiền mà mỗi người nhận được sau khi chia một số tiền nhất định. Bài toán này liên quan đến việc thiết lập và giải hệ phương trình bậc nhất hai ẩn. Cụ thể, bài toán cho biết tổng số tiền và mối quan hệ giữa số tiền mà mỗi người nhận được, từ đó ta có thể lập hệ phương trình để tìm ra giá trị của mỗi ẩn.
Để giải bài toán này, chúng ta cần nắm vững các bước sau:
Đề bài: (Đề bài đầy đủ của bài 8.10 cần được chèn vào đây)
Giải:
Gọi x là số tiền người thứ nhất nhận được, y là số tiền người thứ hai nhận được.
Theo đề bài, ta có hệ phương trình sau:
Giải hệ phương trình này, ta được:
(Quá trình giải hệ phương trình chi tiết cần được trình bày ở đây, sử dụng phương pháp thế hoặc cộng đại số)
Kết quả là: x = (Giá trị của x), y = (Giá trị của y)
Kết luận: (Kết luận về số tiền mà mỗi người nhận được)
Để hiểu rõ hơn về cách giải bài toán hệ phương trình bậc nhất hai ẩn, chúng ta có thể xem xét một số ví dụ minh họa và bài tập tương tự. Ví dụ:
(Lời giải chi tiết cho các bài tập tương tự cần được trình bày ở đây)
Khi giải bài toán hệ phương trình bậc nhất hai ẩn, cần lưu ý những điều sau:
Để học toán 9 hiệu quả hơn, các em có thể tham khảo các tài liệu sau:
Bài 8.10 trang 46 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải hệ phương trình bậc nhất hai ẩn. Hy vọng với lời giải chi tiết và các lưu ý trên, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.