Bài 7.8 trang 26 sách bài tập toán 9 Kết nối tri thức là một bài tập quan trọng trong chương trình học toán 9. Bài tập này yêu cầu học sinh vận dụng kiến thức về hệ phương trình bậc nhất hai ẩn để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.8 trang 26 sách bài tập toán 9 Kết nối tri thức tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Thống kê số ngày nằm viện của 20 bệnh nhân thu được kết quả như sau: 5, 7, 4, 6, 8, 10, 6, 7, 8, 8, 6, 5, 8, 5, 4, 6, 5, 7, 4, 6 a) Lập bảng tần số cho dãy số liệu trên. b) Vẽ biểu đồ tần số dạng đoạn thẳng biểu diễn bảng tần số thu được ở câu a.
Đề bài
Thống kê số ngày nằm viện của 20 bệnh nhân thu được kết quả như sau:
5, 7, 4, 6, 8, 10, 6, 7, 8, 8, 6, 5, 8, 5, 4, 6, 5, 7, 4, 6
a) Lập bảng tần số cho dãy số liệu trên.
b) Vẽ biểu đồ tần số dạng đoạn thẳng biểu diễn bảng tần số thu được ở câu a.
Phương pháp giải - Xem chi tiết
a) Bảng tần số có dạng bảng sau:

Trong đó, \({m_1}\) là tần số của \({x_1}\), \({m_2}\) là tần số của \({x_2}\),…, \({m_k}\) là tần số của \({x_k}\).
Trong bảng tần số, ta chỉ liệt kê các giá trị \({x_i}\) khác nhau, các giá trị \({x_i}\) này có thể không là số.
b) Cách vẽ biểu đồ tần số dạng đoạn thẳng:
Bước 1: Vẽ trục ngang để biểu thị các giá trị trong dãy dữ liệu, vẽ trục đứng thể hiện tần số.
Bước 2: Với mỗi giá trị trên trục ngang và tần số tương ứng ta xác định một điểm. Nối các điểm liên tiếp với nhau.
Bước 3: Ghi chú giải cho các trục, các điểm và tiêu đề của biểu đồ.
Lời giải chi tiết
a) Bảng tần số:

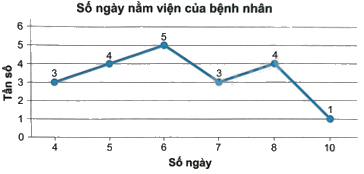
b) Vẽ biểu đồ tần số dạng đoạn thẳng biểu diễn bảng tần số:
Bài 7.8 trang 26 sách bài tập toán 9 Kết nối tri thức tập 2 là một bài toán ứng dụng thực tế, yêu cầu học sinh sử dụng hệ phương trình bậc nhất hai ẩn để giải quyết. Dưới đây là hướng dẫn chi tiết cách giải bài toán này:
Một người đi xe máy từ A đến B với vận tốc 40km/h. Nếu người đó tăng vận tốc thêm 5km/h thì sẽ đến B sớm hơn 18 phút. Tính quãng đường AB.
Bài toán này liên quan đến thời gian, vận tốc và quãng đường. Chúng ta cần xác định các đại lượng chưa biết và thiết lập hệ phương trình để giải quyết.
Quy đồng mẫu số của phương trình, ta được:
9x - 8x = 0.3 * 360
x = 108
Vậy quãng đường AB là 108 km.
Để giải quyết các bài toán tương tự bài 7.8, bạn có thể áp dụng các bước sau:
Hệ phương trình bậc nhất hai ẩn là một công cụ quan trọng trong toán học, được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống. Việc nắm vững kiến thức về hệ phương trình sẽ giúp bạn giải quyết các bài toán thực tế một cách hiệu quả.
Để củng cố kiến thức và kỹ năng giải bài toán hệ phương trình, bạn nên luyện tập thêm các bài toán tương tự trong sách bài tập và các nguồn tài liệu khác. Giaitoan.edu.vn cung cấp nhiều bài giải chi tiết các bài tập toán 9, giúp bạn học toán dễ dàng và hiệu quả hơn.
| Công thức | Mô tả |
|---|---|
| S = v * t | Quãng đường bằng vận tốc nhân thời gian |
| t = S / v | Thời gian bằng quãng đường chia vận tốc |
| v = S / t | Vận tốc bằng quãng đường chia thời gian |
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ hiểu rõ cách giải bài 7.8 trang 26 sách bài tập toán 9 Kết nối tri thức tập 2 và tự tin hơn trong việc học toán.