Bài 9.15 trang 53 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.15 trang 53, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho tam giác ABC có trực tâm H và nội tiếp đường tròn (O). Chứng minh rằng: a) (widehat {OBC} = {90^o} - widehat {BAC}); b) (widehat {BAH} = widehat {OAC}).
Đề bài
Cho tam giác ABC có trực tâm H và nội tiếp đường tròn (O). Chứng minh rằng:
a) \(\widehat {OBC} = {90^o} - \widehat {BAC}\);
b) \(\widehat {BAH} = \widehat {OAC}\).
Phương pháp giải - Xem chi tiết
a) Chứng minh \(\widehat {BAC} = \frac{1}{2}\widehat {BOC}\), \(\widehat {OBC} = {90^o} - \frac{{\widehat {BOC}}}{2}\) nên \(\widehat {OBC} = {90^o} - \widehat {BAC}\).
b) + Chứng minh \(\widehat {OAC} = {90^o} - \widehat {ABC}\).
+ Gọi D là chân đường cao hạ từ đỉnh A của tam giác ABC. Suy ra \(\widehat {BAH} = \widehat {BAD} = {90^o} - \widehat {ABD}\). Do đó, \(\widehat {BAH} = \widehat {OAC}\).
Lời giải chi tiết
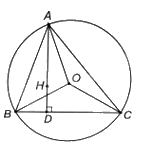
a) Vì góc nội tiếp BAC và góc ở tâm BOC của (O) cùng chắn cung nhỏ BC nên \(\widehat {BAC} = \frac{1}{2}\widehat {BOC}\) (1)
Tam giác BOC có \(OB = OC\) nên tam giác BOC cân tại O. Suy ra \(\widehat {OBC} = \widehat {OCB}\).
Do đó, \(\widehat {OBC} = \frac{{\widehat {OBC} + \widehat {OCB}}}{2} = \frac{1}{2}\left( {{{180}^o} - \widehat {BOC}} \right) = {90^o} - \frac{{\widehat {BOC}}}{2}\) (2)
Từ (1) và (2) ta có: \(\widehat {OBC} = {90^o} - \widehat {BAC}\).
b) Chứng minh tương tự câu a ta có: \(\widehat {OAC} = \frac{1}{2}\left( {{{180}^o} - \widehat {AOC}} \right) = {90^o} - \widehat {ABC}\;\left( 3 \right)\).
Gọi D là chân đường cao hạ từ đỉnh A của tam giác ABC.
Ta có: \(\widehat {BAH} = \widehat {BAD} = {90^o} - \widehat {ABD}\) (vì tam giác ABD vuông tại D) (4).
Từ (3) và (4) ta có: \(\widehat {BAH} = \widehat {OAC}\).
Bài 9.15 thuộc chương Hàm số bậc nhất và hàm số bậc hai, tập trung vào việc ứng dụng kiến thức đã học để giải quyết các bài toán liên quan đến đường thẳng song song và vuông góc. Để giải bài này, học sinh cần nắm vững các khái niệm sau:
Đề bài: (Nội dung đề bài sẽ được chèn vào đây - giả sử đề bài yêu cầu tìm phương trình đường thẳng thỏa mãn điều kiện cho trước)
Hướng dẫn giải:
Ví dụ minh họa: (Ví dụ cụ thể về cách giải bài 9.15, bao gồm các bước giải chi tiết và kết quả cuối cùng)
Ngoài bài 9.15, còn rất nhiều bài tập tương tự trong sách bài tập Toán 9 - Kết nối tri thức tập 2. Để giải quyết các bài tập này, học sinh có thể áp dụng các phương pháp sau:
Để củng cố kiến thức và kỹ năng giải bài tập, học sinh nên luyện tập thêm các bài tập tương tự trong sách bài tập và các đề thi thử. Giaitoan.edu.vn cung cấp nhiều bài tập luyện tập khác với lời giải chi tiết, giúp các em học sinh tự tin hơn trong kỳ thi.
Bài 9.15 trang 53 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng, giúp học sinh rèn luyện kỹ năng giải toán và ứng dụng kiến thức đã học vào thực tế. Hy vọng với lời giải chi tiết và các phương pháp giải được trình bày ở trên, các em học sinh sẽ hiểu rõ hơn về bài tập này và tự tin làm bài tập.
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc nhất | y = ax + b (a ≠ 0) |
| Hàm số bậc hai | y = ax² + bx + c (a ≠ 0) |