Bài 4.8 trang 45 SBT Toán 9 thuộc chương 4: Hệ phương trình bậc nhất hai ẩn. Bài tập này yêu cầu học sinh vận dụng kiến thức về phương pháp giải hệ phương trình để tìm nghiệm của hệ phương trình đã cho.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập Toán 9 hiệu quả.
Vẽ góc (alpha ) trong mỗi trường hợp: a) (cos alpha = 0,4); b) (tan alpha = frac{2}{3}); c) (cot alpha = frac{3}{4}).
Đề bài
Vẽ góc \(\alpha \) trong mỗi trường hợp:
a) \(\cos \alpha = 0,4\);
b) \(\tan \alpha = \frac{2}{3}\);
c) \(\cot \alpha = \frac{3}{4}\).
Phương pháp giải - Xem chi tiết
a) Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \) thì tỉ số giữa cạnh kề và cạnh huyền gọi là cos của \(\alpha \).
Suy ra cách vẽ của góc nhọn \(\alpha \): Vẽ tam giác ABC vuông tại A, \(AB = 2cm\), \(BC = 5cm\). Khi đó, góc ABC là góc \(\alpha \) cần vẽ.
b) Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \) thì tỉ số giữa cạnh đối và cạnh kề gọi là tan của \(\alpha \).
Suy ra cách vẽ của góc nhọn \(\alpha \): Vẽ tam giác ABC vuông tại A, \(AB = 3cm\), \(AC = 2cm\). Khi đó, góc ABC là góc \(\alpha \) cần vẽ.
c) Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \) thì tỉ số giữa cạnh kề và cạnh đối gọi là cot của \(\alpha \).
Suy ra cách vẽ của góc nhọn \(\alpha \):Vẽ tam giác ABC vuông tại A, \(AB = 3cm\), \(AC = 4cm\). Khi đó, góc ABC là góc \(\alpha \) cần vẽ.
Lời giải chi tiết
a) \(\cos \alpha = 0,4 = \frac{2}{5}\)
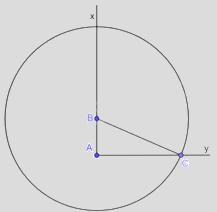
+ Vẽ góc vuông xAy, lấy điểm B thuộc tia Ax sao cho \(AB = 2cm\).
+ Vẽ đường tròn tâm B, bán kính 5cm, đường tròn này cắt tia Ay tại C.
+ Khi đó ta được tam giác ABC vuông tại A, \(AB = 2cm\), \(BC = 5cm\) nên \(\cos \widehat {ABC} = \frac{{AB}}{{BC}} = \frac{2}{5}\).
Vậy góc ABC vẽ như trên thỏa mãn yêu cầu bài toán.
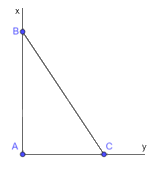
b) + Vẽ góc vuông xAy, lấy điểm B thuộc tia Ax sao cho \(AB = 3cm\).
+ Lấy điểm C thuộc tia Ay sao cho \(AC = 2cm\).
+ Khi đó ta được tam giác ABC vuông tại A, \(AB = 3cm\), \(AC = 2cm\) nên \(\tan \widehat {ABC} = \frac{{AC}}{{AB}} = \frac{2}{3}\).
Vậy góc ABC vẽ như trên thỏa mãn yêu cầu bài toán.
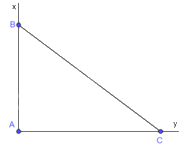
c) + Vẽ góc vuông xAy, lấy điểm B thuộc tia Ax sao cho \(AB = 3cm\).
+ Lấy điểm C thuộc tia Ay sao cho \(AC = 4cm\).
+ Khi đó ta được tam giác ABC vuông tại A, \(AB = 3cm\), \(AC = 4cm\) nên \(\cot \widehat {ABC} = \frac{{AB}}{{AC}} = \frac{3}{4}\).
Vậy góc ABC vẽ như trên thỏa mãn yêu cầu bài toán.
Bài 4.8 trang 45 sách bài tập Toán 9 Kết nối tri thức tập 1 là một bài tập quan trọng trong chương trình học Toán 9, giúp học sinh củng cố kiến thức về hệ phương trình bậc nhất hai ẩn. Để giải bài tập này, học sinh cần nắm vững các phương pháp giải hệ phương trình như phương pháp thế và phương pháp cộng đại số.
Bài tập yêu cầu giải các hệ phương trình sau:
a) { x + y = 5 2x - y = 1
b) { 3x - 2y = 7 x + 2y = 1
c) { x - 2y = -1 2x + y = 5
d) { 5x + 2y = 12 x - y = 1
Có hai phương pháp chính để giải hệ phương trình bậc nhất hai ẩn:
a) Giải hệ phương trình: { x + y = 5 2x - y = 1
Lời giải:
Cộng hai phương trình, ta được: (x + y) + (2x - y) = 5 + 1 => 3x = 6 => x = 2
Thay x = 2 vào phương trình x + y = 5, ta được: 2 + y = 5 => y = 3
Vậy nghiệm của hệ phương trình là (x; y) = (2; 3)
b) Giải hệ phương trình: { 3x - 2y = 7 x + 2y = 1
Lời giải:
Cộng hai phương trình, ta được: (3x - 2y) + (x + 2y) = 7 + 1 => 4x = 8 => x = 2
Thay x = 2 vào phương trình x + 2y = 1, ta được: 2 + 2y = 1 => 2y = -1 => y = -1/2
Vậy nghiệm của hệ phương trình là (x; y) = (2; -1/2)
c) Giải hệ phương trình: { x - 2y = -1 2x + y = 5
Lời giải:
Nhân phương trình thứ nhất với -2, ta được: -2x + 4y = 2
Cộng phương trình mới với phương trình thứ hai, ta được: (-2x + 4y) + (2x + y) = 2 + 5 => 5y = 7 => y = 7/5
Thay y = 7/5 vào phương trình x - 2y = -1, ta được: x - 2(7/5) = -1 => x - 14/5 = -1 => x = 9/5
Vậy nghiệm của hệ phương trình là (x; y) = (9/5; 7/5)
d) Giải hệ phương trình: { 5x + 2y = 12 x - y = 1
Lời giải:
Nhân phương trình thứ hai với 2, ta được: 2x - 2y = 2
Cộng phương trình mới với phương trình thứ nhất, ta được: (5x + 2y) + (2x - 2y) = 12 + 2 => 7x = 14 => x = 2
Thay x = 2 vào phương trình x - y = 1, ta được: 2 - y = 1 => y = 1
Vậy nghiệm của hệ phương trình là (x; y) = (2; 1)
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ tự tin hơn khi giải bài tập 4.8 trang 45 sách bài tập Toán 9 Kết nối tri thức tập 1. Chúc các em học tốt!