Bài 10.7 trang 66 sách bài tập toán 9 thuộc chương trình Kết nối tri thức tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về ứng dụng tỉ số lượng giác vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 10.7 này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
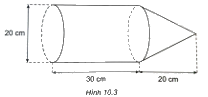
Bác Khôi làm một dụng cụ bằng tôn gồm một phần có dạng hình trụ và một phần có dạng hình nón với các kích thước như Hình 10.3. Tính thể tích của dụng cụ này (coi mép hàn không đáng kể và làm tròn kết quả đến hàng đơn vị của (c{m^3})).
Đề bài
Bác Khôi làm một dụng cụ bằng tôn gồm một phần có dạng hình trụ và một phần có dạng hình nón với các kích thước như Hình 10.3. Tính thể tích của dụng cụ này (coi mép hàn không đáng kể và làm tròn kết quả đến hàng đơn vị của \(c{m^3}\)).
Phương pháp giải - Xem chi tiết
Thể tích của hình trụ có bán kính đáy R và chiều cao h là:
\({{V}_{1}}={{S}_{đáy}}.h=\pi {{R}^{2}}h\).
Thể tích của hình nón bán kính r và chiều cao h là:
\({V_2} = \frac{1}{3}\pi {r^2}h\).
Thể tích của dụng cụ là:
\(V = {V_1} + {V_2}\).
Lời giải chi tiết
Thể tích của hình trụ là:
\({V_1} = \pi .{\left( {20:2} \right)^2}.30 = 3\;000\pi \left( {c{m^3}} \right)\).
Thể tích của hình nón là:
\({V_2} = \frac{1}{3}.\pi .{\left( {20:2} \right)^2}.20 = \frac{{2\;000\pi }}{3}\left( {c{m^3}} \right)\).
Thể tích của dụng cụ là:
\(V = {V_1} + {V_2} = 3\;000\pi + \frac{{2\;000\pi }}{3} = \frac{{11\;000\pi }}{3} \approx 11\;519\left( {c{m^3}} \right).\)
Bài 10.7 yêu cầu chúng ta giải quyết một bài toán liên quan đến chiều cao của một ngọn cây và góc tạo bởi tia nắng mặt trời. Để giải bài toán này, chúng ta cần hiểu rõ về các tỉ số lượng giác cơ bản (sin, cos, tan) và cách áp dụng chúng vào tam giác vuông.
Gọi chiều cao của ngọn cây là h (m). Ta có tam giác vuông với góc 60° tại đỉnh của ngọn cây, cạnh đối là h và cạnh kề là 10m.
Áp dụng tỉ số lượng giác tan, ta có:
tan(60°) = h / 10
Suy ra: h = 10 * tan(60°)
Vì tan(60°) = √3, nên:
h = 10 * √3 ≈ 17.32 (m)
Vậy, chiều cao của ngọn cây là khoảng 17.32 mét.
Trong bài toán này, việc xác định đúng cạnh đối và cạnh kề là rất quan trọng. Cạnh đối là cạnh nằm đối diện với góc đang xét (60°), và cạnh kề là cạnh nằm kề với góc đang xét. Việc sử dụng đúng tỉ số lượng giác (tan, sin, cos) sẽ giúp chúng ta tìm ra mối liên hệ giữa các cạnh và góc trong tam giác vuông.
Các bài tập tương tự bài 10.7 thường yêu cầu tính chiều cao của các vật thể (như cột điện, tòa nhà) hoặc khoảng cách giữa hai điểm, dựa vào góc tạo bởi tia nhìn và các cạnh của tam giác vuông. Để giải các bài tập này, chúng ta cần:
Ngoài việc áp dụng tỉ số lượng giác vào giải toán, chúng ta còn có thể sử dụng chúng trong nhiều lĩnh vực khác của đời sống, như đo đạc khoảng cách, tính góc nâng, góc hạ, và xây dựng các mô hình không gian.
Bài 10.7 trang 66 sách bài tập toán 9 - Kết nối tri thức tập 2 là một bài tập điển hình để rèn luyện kỹ năng áp dụng tỉ số lượng giác vào giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và các giải thích trên, các em học sinh đã hiểu rõ cách giải bài toán này và có thể tự tin giải các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!