Bài 9.43 trang 60 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài toán quan trọng trong chương trình học. Bài toán này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài tập thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.43 trang 60, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho O là trung điểm của đoạn thẳng AB. a) Tìm một phép quay biến điểm A thành điểm B và biến điểm B thành điểm A. b) Phép quay thuận chiều ({90^o}) tâm O biến A thành C và biến B thành D. Chứng tỏ rằng ACBD là một hình vuông.
Đề bài
Cho O là trung điểm của đoạn thẳng AB.
a) Tìm một phép quay biến điểm A thành điểm B và biến điểm B thành điểm A.
b) Phép quay thuận chiều \({90^o}\) tâm O biến A thành C và biến B thành D. Chứng tỏ rằng ACBD là một hình vuông.
Phương pháp giải - Xem chi tiết
a) Phép quay thuận chiều \({\alpha ^o}\left( {{0^o} < {\alpha ^o} < {{360}^o}} \right)\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \({\alpha ^o}\).
b) + Chứng minh tứ giác ABCD nội tiếp đường tròn (O), bán kính \(\frac{{AB}}{2}\).
+ Chứng minh CD là đường kính của (O), suy ra \(\widehat {ACB} = \widehat {CBD} = \widehat {BDA} = \widehat {DAC} = {90^o}\) nên ACBD là hình chữ nhật (1).
+ \(\Delta AOC = \Delta COB = \Delta BOD = \Delta DOA\) nên \(AC = CB = BD = DA\) (2).
+ Từ (1) và (2) suy ra ACBD là hình vuông.
Lời giải chi tiết
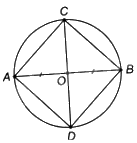
a) Phép quay thuận chiều \({180^o}\) tâm O biến điểm A thành B và biến B thành A.
b) Vì \(OA = OB = OC = OD\) nên tứ giác ABCD nội tiếp đường tròn (O), bán kính \(\frac{{AB}}{2}\).
Vì \(\widehat {AOC} = \widehat {BOD} = {90^o}\) nên OC và OD cùng vuông góc với AB. Do đó, O, C, D thẳng hàng. Suy ra, CD là đường kính của (O). Suy ra, \(\widehat {ACB} = \widehat {CBD} = \widehat {BDA} = \widehat {DAC} = {90^o}\) (các góc nội tiếp chắn nửa đường tròn của (O)). Suy ra, ACBD là hình chữ nhật (1).
Hơn nữa, \(\Delta AOC = \Delta COB = \Delta BOD = \Delta DOA\) (các tam giác vuông cân tại đỉnh O có các cạnh góc vuông bằng nhau) nên \(AC = CB = BD = DA\) (2).
Từ (1) và (2) ta có: ACBD là hình vuông.
Bài 9.43 trang 60 sách bài tập Toán 9 - Kết nối tri thức tập 2 yêu cầu chúng ta xét hàm số bậc hai và tìm các điểm thuộc đồ thị hàm số. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về hàm số bậc hai, bao gồm:
Nội dung bài toán:
Cho hàm số y = x2 - 4x + 3. Tìm tọa độ các điểm A, B thuộc đồ thị hàm số sao cho A có hoành độ x = -1 và B có tung độ y = 0.
Để tìm tọa độ điểm A, ta thay x = -1 vào hàm số y = x2 - 4x + 3:
y = (-1)2 - 4(-1) + 3 = 1 + 4 + 3 = 8
Vậy tọa độ điểm A là (-1; 8).
Để tìm tọa độ điểm B, ta thay y = 0 vào hàm số y = x2 - 4x + 3:
0 = x2 - 4x + 3
Giải phương trình bậc hai này, ta được:
Δ = (-4)2 - 4(1)(3) = 16 - 12 = 4
x1 = (4 + √4) / 2 = (4 + 2) / 2 = 3
x2 = (4 - √4) / 2 = (4 - 2) / 2 = 1
Vậy có hai điểm B thỏa mãn điều kiện, là B1(3; 0) và B2(1; 0).
Tọa độ các điểm A, B thuộc đồ thị hàm số y = x2 - 4x + 3 là:
Để hiểu rõ hơn về hàm số bậc hai và cách giải các bài toán liên quan, các em có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 9 - Kết nối tri thức tập 2. Ngoài ra, các em cũng có thể tìm kiếm các tài liệu học tập trực tuyến hoặc tham gia các khóa học toán online để nâng cao kiến thức và kỹ năng giải toán.
Một số bài tập tương tự mà các em có thể luyện tập:
Khi giải các bài tập về hàm số bậc hai, các em cần lưu ý những điều sau:
Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải bài 9.43 trang 60 sách bài tập Toán 9 - Kết nối tri thức tập 2. Chúc các em học tập tốt!