Bài 9.52 trang 62 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.52, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho tam giác nhọn ABC (AB<AC) có các đường cao AD, BE, CF. Cho EF cắt BC tại K. Chứng minh rằng: a) KB. KC = KE. KF; b) (frac{{KB}}{{KC}} = frac{{DB}}{{DC}}).
Đề bài
Cho tam giác nhọn ABC (AB<AC) có các đường cao AD, BE, CF. Cho EF cắt BC tại K. Chứng minh rằng:
a) KB. KC = KE. KF;
b) \(\frac{{KB}}{{KC}} = \frac{{DB}}{{DC}}\).
Phương pháp giải - Xem chi tiết
a) + Chứng minh tứ BFEC nội tiếp đường tròn đường kính BC, suy ra \(\widehat {KFB} = {180^o} - \widehat {BFE} = \widehat {BCE}\).
+ Chứng minh $\Delta KFB\backsim \Delta KCE\left( g.g \right)$, suy ra KB. KC = KE. KF.
b) + Chứng minh $\Delta KEB\backsim \Delta KCF\left( g.g \right)$, suy ra \(\frac{{KE}}{{KC}} = \frac{{EB}}{{CF}}\).
+ Chứng minh \(\frac{{KB}}{{KE}} = \frac{{FB}}{{CE}}\) suy ra \(\frac{{KB}}{{KC}} = \frac{{KB}}{{KE}}.\frac{{KE}}{{KC}} = \frac{{BF}}{{CF}}.\frac{{BE}}{{CE}}\) (1)
+ Chứng minh $\Delta BDF\backsim \Delta BAC\left( g.g \right)$ nên \(\frac{{DB}}{{AB}} = \frac{{BF}}{{BC}}\), tương tự ta có \(\frac{{DC}}{{AC}} = \frac{{CE}}{{BC}}\) nên \(\frac{{DB}}{{DC}} = \frac{{BF}}{{CE}}.\frac{{AB}}{{AC}}\) (2)
+ Chứng minh $\Delta ABE\backsim \Delta ACF$, suy ra \(\frac{{AB}}{{AC}} = \frac{{BE}}{{CF}}\) (3).
+ Từ (1), (2) và (3) suy ra điều phải chứng minh.
Lời giải chi tiết
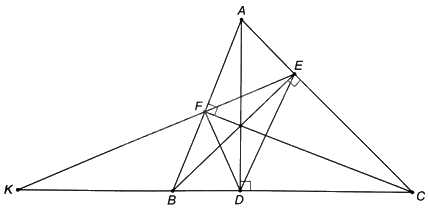
a) Vì \(\widehat {BFC} = \widehat {BEC} = {90^o}\) nên tứ giác BFEC nội tiếp đường tròn đường kính BC.
Chứng minh tương tự ta có: tứ giác AFDC nội tiếp đường tròn đường kính AC, tứ giác AEDB nội tiếp đường tròn đường kính AB.
Vì tứ giác BFEC nội tiếp đường tròn đường kính BC nên \(\widehat {KFB} = {180^o} - \widehat {BFE} = \widehat {BCE}\).
Tam giác KFB và tam giác KCE có: \(\widehat {KFB} = \widehat {BCE}\), góc K chung.
Suy ra: $\Delta KFB\backsim \Delta KCE\left( g.g \right)$. Suy ra, \(\frac{{KF}}{{KC}} = \frac{{KB}}{{KE}}\), hay KB. KC = KE. KF.
b) Hai tam giác KEB và tam giác KCF có: \(\widehat {KEB} = \widehat {KCF}\) (hai góc nội tiếp cùng chắn cung BF của đường tròn đường kính BC), góc K chung nên $\Delta KEB\backsim \Delta KCF\left( g.g \right)$, suy ra \(\frac{{KE}}{{KC}} = \frac{{EB}}{{CF}}\).
Mặt khác: \(\frac{{KB}}{{KE}} = \frac{{FB}}{{CE}}\) (do $\Delta KFB\backsim \Delta KCE\left( cmt \right)$). Suy ra: \(\frac{{KB}}{{KC}} = \frac{{KB}}{{KE}}.\frac{{KE}}{{KC}} = \frac{{BF}}{{CF}}.\frac{{BE}}{{CE}}\) (1)
Chứng minh tương tự ta có: hai tam giác BDF và tam giác BAC có:
\(\widehat {BDF} = {180^o} - \widehat {FDC} = \widehat {BAC};\widehat {DBF} = \widehat {ABC}\).
Suy ra: $\Delta BDF\backsim \Delta BAC\left( g.g \right)$, suy ra \(\frac{{DB}}{{AB}} = \frac{{BF}}{{BC}}\). Tương tự ta có: \(\frac{{DC}}{{AC}} = \frac{{CE}}{{BC}}\) nên \(\frac{{DB}}{{DC}} = \frac{{BF}}{{CE}}.\frac{{AB}}{{AC}}\) (2)
Mà $\Delta ABE\backsim \Delta ACF$ (hai tam giác vuông có chung góc nhọn BAC). Do đó, \(\frac{{AB}}{{AC}} = \frac{{BE}}{{CF}}\) (3).
Từ (1), (2) và (3) ta có: \(\frac{{KB}}{{KC}} = \frac{{DB}}{{DC}}\).
Bài 9.52 thuộc chương Hàm số bậc hai, một trong những chương quan trọng của Toán 9. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về:
Bài 9.52 thường yêu cầu học sinh thực hiện các thao tác sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 9.52, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể. Giả sử bài toán yêu cầu:
“Cho hàm số y = x2 - 4x + 3. Hãy tìm tọa độ đỉnh của parabol và vẽ đồ thị hàm số.”
Trong hàm số y = x2 - 4x + 3, ta có:
Tọa độ đỉnh của parabol có dạng (x0; y0), trong đó:
Vậy tọa độ đỉnh của parabol là (2; -1).
Để vẽ đồ thị hàm số, ta thực hiện các bước sau:
Ngoài bài 9.52, còn rất nhiều bài tập tương tự trong sách bài tập Toán 9 - Kết nối tri thức tập 2. Các em có thể tham khảo thêm các bài tập sau:
Để học tốt chương Hàm số bậc hai, các em cần:
Bài 9.52 trang 62 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về hàm số bậc hai. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em sẽ tự tin hơn khi giải quyết các bài toán tương tự.