Bài 5.31 trang 71 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5.31 trang 71, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Từ điểm P nằm ngoài đường tròn (O), kẻ hai tiếp tuyến PA và PB đến đường tròn (A và B là hai tiếp điểm). a) Chứng minh rằng (PO bot AB). b) Gọi C là điểm đối xứng với A qua O. Chứng minh rằng BC//PO. c) Tính độ dài các cạnh của tam giác PAB, biết OA=3cm và OP=5cm.
Đề bài
Từ điểm P nằm ngoài đường tròn (O), kẻ hai tiếp tuyến PA và PB đến đường tròn (A và B là hai tiếp điểm).
a) Chứng minh rằng \(PO \bot AB\).
b) Gọi C là điểm đối xứng với A qua O. Chứng minh rằng BC//PO.
c) Tính độ dài các cạnh của tam giác PAB, biết OA=3cm và OP=5cm.
Phương pháp giải - Xem chi tiết
a) + Chứng minh \(PA = PB\) và PO là tia phân giác của góc APB.
+ Chứng minh tam giác PAB cân tại P, suy ra PO là đường trung trực của tam giác AP nên \(PO \bot AB\).
b) + Chứng minh C thuộc (O).
+ Chứng minh tam giác ABC vuông tại B. Do đó, \(BA \bot BC\). Mà \(PO \bot AB\)(cmt) nên BC//PO.
c) + Chứng minh \(PA \bot OA\).
+ Áp dụng định lí Pythagore vào tam giác OAP vuông tại tính được PA, suy ra, \(PA = PB = 4cm\).
+ Gọi H là giao điểm của PO và AB. Theo a ta có: \(AH \bot OP\) và \(AB = 2AH\).
+ \(AH.OP = OA.PA\left( { = 2{S_{\Delta AOP}}} \right)\) nên \(AH = \frac{{OA.AP}}{{OP}}\) nên tính được AB.
Lời giải chi tiết
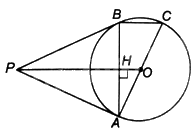
a) Vì PA và PB là hai tiếp tuyến cắt nhau tại P của (O) nên \(PA = PB\), PO là tia phân giác của góc APB.
Vì \(PA = PB\) nên tam giác PAB cân tại P. Do đó, PO là đường phân giác đồng thời là đường trung trực của tam giác ABP. Suy ra: \(PO \bot AB\).
b) Vì C là điểm đối xứng với A qua O nên \(OA = OC\). Do đó, C thuộc (O).
Vì \(OB = OC = OA = \frac{1}{2}AC\) nên tam giác BAC có trung tuyến BO có độ dài bằng nửa độ dài cạnh AC nên tam giác ABC vuông tại B. Do đó, \(BA \bot BC\). Mà \(PO \bot AB\)(cmt) nên BC//PO.
c) Vì PA tiếp xúc với (O) tại A nên \(PA \bot OA\).
Áp dụng định lí Pythagore vào tam giác OAP vuông tại A có: \(O{A^2} + A{P^2} = O{P^2}\) nên \(PA = \sqrt {O{P^2} - O{A^2}} = \sqrt {{5^2} - {3^2}} = 4\left( {cm} \right)\)
Do đó, \(PA = PB = 4cm\)
Gọi H là giao điểm của PO và AB. Theo a ta có: \(AH \bot OP\) và \(AB = 2AH\).
Ta có: \(AH.OP = OA.PA\left( { = 2{S_{\Delta AOP}}} \right)\) nên \(AH = \frac{{OA.AP}}{{OP}} = \frac{{3.4}}{5} = 2,4\left( {cm} \right)\).
Do đó, \(AB = 2AH = 2.2,4 = 4,8\left( {cm} \right)\).
Trước khi đi vào giải chi tiết bài 5.31, chúng ta cùng ôn lại một số kiến thức cơ bản về hàm số bậc nhất và hàm số bậc hai. Hàm số bậc nhất có dạng y = ax + b (a ≠ 0), trong đó a là hệ số góc và b là tung độ gốc. Hàm số bậc hai có dạng y = ax² + bx + c (a ≠ 0), trong đó a, b, c là các hệ số. Việc hiểu rõ các tính chất của hàm số, đặc biệt là đồ thị hàm số, là rất quan trọng để giải quyết các bài toán liên quan.
Đề bài 5.31 thường yêu cầu học sinh xác định hàm số, tìm các điểm thuộc đồ thị hàm số, hoặc giải các bài toán ứng dụng liên quan đến hàm số. Để giải bài tập này, cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, vận dụng các kiến thức đã học để xây dựng phương trình hoặc hệ phương trình phù hợp.
(Phần này sẽ chứa lời giải chi tiết của bài 5.31, bao gồm các bước giải, giải thích rõ ràng và các ví dụ minh họa. Lời giải sẽ được trình bày một cách logic và dễ hiểu, giúp học sinh nắm vững phương pháp giải.)
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 5.31, chúng ta cùng xem xét một số ví dụ minh họa và bài tập tương tự. Các ví dụ này sẽ giúp các em củng cố kiến thức và rèn luyện kỹ năng giải toán.
Khi giải bài tập về hàm số, cần lưu ý một số điểm sau:
Hàm số có rất nhiều ứng dụng trong thực tế, ví dụ như:
Bài 5.31 trang 71 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số. Hy vọng rằng với lời giải chi tiết và các ví dụ minh họa, các em học sinh sẽ hiểu rõ phương pháp giải và tự tin làm bài tập. Chúc các em học tốt!
| Công thức | Mô tả |
|---|---|
| y = ax + b | Hàm số bậc nhất |
| y = ax² + bx + c | Hàm số bậc hai |
| x0 = -b/2a | Hoành độ đỉnh của parabol |