Bài 9.25 trang 56 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.25 trang 56, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho tứ giác ABCD nội tiếp đường tròn (O) sao cho hai tia AB và DC cắt nhau tại điểm I. Chứng minh rằng: a) $Delta IADbacksim Delta ICB,Delta IACbacksim Delta IDB$; b) (frac{{IC}}{{ID}} = frac{{AC}}{{AD}}.frac{{BC}}{{BD}}).
Đề bài
Cho tứ giác ABCD nội tiếp đường tròn (O) sao cho hai tia AB và DC cắt nhau tại điểm I. Chứng minh rằng:
a) $\Delta IAD\backsim \Delta ICB,\Delta IAC\backsim \Delta IDB$;
b) \(\frac{{IC}}{{ID}} = \frac{{AC}}{{AD}}.\frac{{BC}}{{BD}}\).
Phương pháp giải - Xem chi tiết
a) + Chứng minh \(\widehat {IAD} = \widehat {ICB}\), từ đó chứng minh được $\Delta IAD\backsim \Delta ICB\left( g.g \right)$.
+ Chứng minh \(\widehat {IAC} = \widehat {IDB}\), từ đó chứng minh được $\Delta IAC\backsim \Delta IDB\left( g.g \right)$.
b) Từ a ta suy ra: \(\frac{{IC}}{{IA}} = \frac{{BC}}{{AD}}\), \(\frac{{IA}}{{ID}} = \frac{{AC}}{{BD}}\). Do đó, \(\frac{{IC}}{{ID}} = \frac{{IC}}{{IA}}.\frac{{IA}}{{ID}} = \frac{{AC}}{{AD}}.\frac{{BC}}{{BD}}\).
Lời giải chi tiết
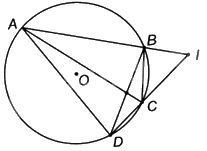
a) Vì tứ giác ABCD nội tiếp (O) nên \(\widehat {IAD} + \widehat {BCD} = {180^o}\). Mà \(\widehat {ICB} + \widehat {BCD} = {180^o}\) nên \(\widehat {IAD} = \widehat {ICB}\).
Tam giác IAD và tam giác ICB có: góc I chung, \(\widehat {IAD} = \widehat {ICB}\) nên $\Delta IAD\backsim \Delta ICB\left( g.g \right)$.
Tam giác IAC và tam giác IDB có: góc I chung, \(\widehat {IAC} = \widehat {IDB}\) (hai góc nội tiếp (O) cùng chắn cung BC)
Do đó, $\Delta IAC\backsim \Delta IDB\left( g.g \right)$.
b) Vì $\Delta IAD\backsim \Delta ICB$ nên \(\frac{{IC}}{{IA}} = \frac{{BC}}{{AD}}\); $\Delta IAC\backsim \Delta IDB$ nên \(\frac{{IA}}{{ID}} = \frac{{AC}}{{BD}}\).
Do đó, \(\frac{{IC}}{{ID}} = \frac{{IC}}{{IA}}.\frac{{IA}}{{ID}} = \frac{{AC}}{{AD}}.\frac{{BC}}{{BD}}\).
Bài 9.25 thuộc chương Hàm số bậc nhất và hàm số bậc hai, tập trung vào việc ứng dụng kiến thức đã học để giải quyết các bài toán liên quan đến đường thẳng song song và vuông góc. Để giải bài này, học sinh cần nắm vững các khái niệm sau:
Đề bài: (Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho hai đường thẳng d₁: y = 2x + 1 và d₂: y = -x + 4. Tìm tọa độ giao điểm của hai đường thẳng này.)
Lời giải:
Ta có hệ phương trình:
{ y = 2x + 1 y = -x + 4 }
Thay y = 2x + 1 vào phương trình thứ hai, ta được:
2x + 1 = -x + 4
3x = 3
x = 1
Thay x = 1 vào phương trình y = 2x + 1, ta được:
y = 2 * 1 + 1 = 3
Vậy tọa độ giao điểm của hai đường thẳng là (1; 3).
Ngoài bài 9.25, còn rất nhiều bài tập tương tự trong sách bài tập Toán 9 - Kết nối tri thức tập 2. Các bài tập này thường yêu cầu học sinh:
Để giải các bài tập này, học sinh cần nắm vững lý thuyết và luyện tập thường xuyên. Giaitoan.edu.vn cung cấp đầy đủ các bài giải chi tiết và bài tập luyện tập để giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Hàm số bậc nhất và hàm số bậc hai có rất nhiều ứng dụng trong thực tế, ví dụ như:
Việc hiểu rõ về hàm số bậc nhất và hàm số bậc hai không chỉ giúp học sinh giải quyết các bài tập toán học mà còn giúp các em ứng dụng kiến thức vào cuộc sống thực tế.
Để củng cố kiến thức về bài 9.25 và các bài tập tương tự, các em học sinh có thể tham khảo thêm các bài tập sau:
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và những kiến thức bổ ích trên, các em học sinh sẽ hiểu rõ hơn về bài 9.25 trang 56 Sách bài tập Toán 9 - Kết nối tri thức tập 2 và tự tin hơn trong quá trình học tập.