Bài 4.37 trang 53 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.37 trang 53, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
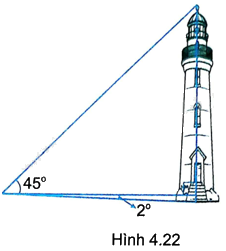
Một người đứng cách chân ngọn hải đăng 50m, nhìn xuống chân hải đăng dưới góc ({2^o}) và nhìn lên đỉnh ngọn hải đăng dưới góc ({45^o}) (so với phương nằm ngang) (H.4.22). Tính chiều cao ngọn hải đăng (làm tròn đến mét).
Đề bài
Một người đứng cách chân ngọn hải đăng 50m, nhìn xuống chân hải đăng dưới góc \({2^o}\) và nhìn lên đỉnh ngọn hải đăng dưới góc \({45^o}\) (so với phương nằm ngang) (H.4.22). Tính chiều cao ngọn hải đăng (làm tròn đến mét).
Phương pháp giải - Xem chi tiết
+ Gọi chân hải đăng ở vị trí điểm A, đỉnh hải đăng ở vị trí điểm B, đầu người quan sát ở vị trí điểm C,
H là hình chiếu vuông góc của C trên đường thẳng AB.
+ Chỉ ra H nằm giữa A và B.
+ Tam giác ACH vuông tại H nên \(AH = CH\tan {2^o}\).
+ Chứng minh tam giác BCH vuông cân tại H nên \(HB = HC\).
+ \(AB = AH + HB\) nên tính được AB.
Lời giải chi tiết
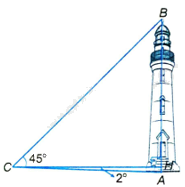
Gọi chân hải đăng ở vị trí điểm A, đỉnh hải đăng ở vị trí điểm B, đầu người quan sát ở vị trí điểm C.
Gọi H là hình chiếu vuông góc của C trên đường thẳng AB thì theo giả thiết, ta có H nằm giữa A và B, \(CH = 50m\).
Tam giác ACH vuông tại H, \(\widehat {ACH} = {2^o}\) nên \(AH = CH\tan {2^o} = 50\tan {2^o}\)
Tam giác CBH vuông tại H, \(\widehat {BCH} = {45^o}\) nên tam giác CBH vuông cân tại H, do đó \(HB = HC = 50m\)
Suy ra \(AB = AH + HB = 50\left( {\tan {2^o} + 1} \right) \approx 52\left( m \right)\)
Trước khi đi vào giải chi tiết bài 4.37, chúng ta cùng ôn lại một số kiến thức cơ bản về hàm số bậc nhất và hàm số bậc hai. Hàm số bậc nhất có dạng y = ax + b (a ≠ 0), trong đó a là hệ số góc và b là tung độ gốc. Hàm số bậc hai có dạng y = ax² + bx + c (a ≠ 0), trong đó a, b, c là các hệ số. Việc hiểu rõ các tính chất của hàm số, đặc biệt là cách xác định hệ số và vẽ đồ thị hàm số, là rất quan trọng để giải quyết các bài toán liên quan.
Đề bài 4.37 thường yêu cầu học sinh xác định hàm số dựa trên các thông tin cho trước, hoặc giải các bài toán ứng dụng liên quan đến hàm số. Để giải bài tập này, cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, vận dụng kiến thức về hàm số để xây dựng phương trình hoặc hệ phương trình phù hợp, và giải để tìm ra kết quả.
(Phần này sẽ chứa lời giải chi tiết của bài 4.37, bao gồm các bước giải, giải thích rõ ràng và các lưu ý quan trọng. Ví dụ:)
Bài 4.37: Cho hàm số y = 2x + 3. Hãy tìm giá trị của y khi x = -1; x = 0; x = 2.
Vậy, khi x = -1 thì y = 1; khi x = 0 thì y = 3; khi x = 2 thì y = 7.
Ngoài bài 4.37, còn rất nhiều bài tập tương tự liên quan đến hàm số bậc nhất và hàm số bậc hai. Một số dạng bài tập thường gặp bao gồm:
Để giải các bài tập này, cần nắm vững các kiến thức về hàm số, đặc biệt là cách xác định hệ số, vẽ đồ thị và giải phương trình. Ngoài ra, cần luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Hàm số có rất nhiều ứng dụng trong thực tế, ví dụ như trong kinh tế, tài chính, vật lý, kỹ thuật,... Trong kinh tế, hàm số được sử dụng để mô tả mối quan hệ giữa cung và cầu, chi phí và doanh thu. Trong vật lý, hàm số được sử dụng để mô tả chuyển động của các vật thể, sự biến đổi của các đại lượng vật lý. Việc hiểu rõ ứng dụng của hàm số giúp chúng ta có cái nhìn sâu sắc hơn về thế giới xung quanh.
Để củng cố kiến thức về hàm số, các em có thể làm thêm một số bài tập sau:
Bài 4.37 trang 53 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ hiểu rõ phương pháp giải và tự tin làm bài tập. Chúc các em học tốt!