Bài 10.17 trang 71 SBT Toán 9 thuộc chương trình Toán 9 Kết nối tri thức tập 2, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này thường gặp trong các kỳ thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 10.17 trang 71 SBT Toán 9, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
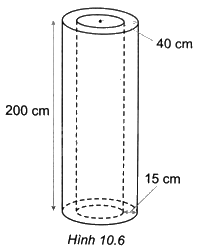
Người ta cần làm một ống thoát nước hình trụ bằng bê tông (H.10.6) có chiều cao là 200cm, độ dày của thành ống là 15cm, đường kính của ống là 80cm. Tính lượng bê tông cần dùng để làm ống thoát nước nói trên.
Đề bài
Người ta cần làm một ống thoát nước hình trụ bằng bê tông (H.10.6) có chiều cao là 200cm, độ dày của thành ống là 15cm, đường kính của ống là 80cm. Tính lượng bê tông cần dùng để làm ống thoát nước nói trên.
Phương pháp giải - Xem chi tiết
+ Lượng bê tông cần dùng để làm ống thoát nước bằng thể tích hình trụ bán kính 40cm, chiều cao 200m trừ đi thể tích hình trụ bán kính 25cm, chiều cao 200m.
+ Thể tích của hình trụ có bán kính đáy R và chiều cao h là: \(V={{S}_{đáy}}.h=\pi {{R}^{2}}h\).
Lời giải chi tiết
Thể tích hình trụ lớn là:
\({V_1} = \pi {.40^2}.200 = 320\;000\pi \left( {c{m^3}} \right)\).
Thể tích hình trụ nhỏ là:
\({V_2} = \pi .{\left( {40 - 15} \right)^2}.200 = 125\;000\pi \left( {c{m^3}} \right)\).
Lượng bê tông cần dùng là:
\(V = {V_1} - {V_2} = 320\;000\pi - 125\;000\pi = 195\;000\pi \left( {c{m^3}} \right).\)
Bài 10.17 sách bài tập Toán 9 Kết nối tri thức tập 2 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc hai. Cụ thể, bài toán thường mô tả một tình huống trong đó một đại lượng thay đổi theo một hàm số bậc hai, và yêu cầu học sinh tìm các thông số của hàm số hoặc giải các bài toán liên quan đến giá trị của hàm số.
Để giải bài 10.17 trang 71 SBT Toán 9, học sinh cần nắm vững các kiến thức sau:
Phương pháp giải bài toán thường bao gồm các bước sau:
(Nội dung lời giải chi tiết sẽ được trình bày tại đây, bao gồm các bước giải cụ thể, các phép tính và giải thích rõ ràng. Ví dụ:)
Bài 10.17: Một quả bóng được ném lên từ mặt đất với vận tốc ban đầu là 15 m/s. Giả sử rằng quả bóng chuyển động theo một quỹ đạo parabol. Hãy viết phương trình mô tả quỹ đạo của quả bóng, biết rằng gia tốc trọng trường là g = 9.8 m/s2.
Giải:
Gọi x là khoảng cách ngang từ vị trí ném đến vị trí của quả bóng, và y là độ cao của quả bóng so với mặt đất. Ta có thể mô tả quỹ đạo của quả bóng bằng phương trình:
y = - (g/2v02cos2θ)x2 + (tan θ)x
Trong đó:
Thay các giá trị vào phương trình, ta được:
y = - (9.8 / (2 * 152 * cos245o))x2 + (tan 45o)x
y = - 0.0229x2 + x
Vậy phương trình mô tả quỹ đạo của quả bóng là y = - 0.0229x2 + x.
Để củng cố kiến thức về hàm số bậc hai và rèn luyện kỹ năng giải bài tập, học sinh có thể tham khảo các bài tập tương tự sau:
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết bài 10.17 trang 71 SBT Toán 9 - Kết nối tri thức tập 2 sẽ giúp các em học sinh hiểu rõ hơn về hàm số bậc hai và tự tin giải các bài tập tương tự. Chúc các em học tập tốt!
| Hàm số | Đỉnh | Trục đối xứng |
|---|---|---|
| y = ax2 + bx + c | I(-b/2a; (4ac - b2)/4a) | x = -b/2a |