Bài 12 trang 73 Sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học Toán 9. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 12 trang 73 Sách bài tập Toán 9 - Kết nối tri thức tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho tam giác nhọn ABC và điểm D nằm giữa B và C. Gọi E và F lần lượt là chân đường vuông góc hạ từ D xuống AB và AC. a) Gọi I và J lần lượt là tâm đường tròn ngoại tiếp tam giác EBD và tam giác FDC. Chứng minh rằng hai đường tròn (I) và (J) tiếp xúc ngoài với nhau. b) Giả sử M là một điểm tùy ý khác F, nằm giữa A và C; gọi K là tâm đường tròn ngoại tiếp tam giác MDC. Chứng minh rằng hai đường tròn (I) và (K) cắt nhau.
Đề bài
Cho tam giác nhọn ABC và điểm D nằm giữa B và C. Gọi E và F lần lượt là chân đường vuông góc hạ từ D xuống AB và AC.
a) Gọi I và J lần lượt là tâm đường tròn ngoại tiếp tam giác EBD và tam giác FDC. Chứng minh rằng hai đường tròn (I) và (J) tiếp xúc ngoài với nhau.
b) Giả sử M là một điểm tùy ý khác F, nằm giữa A và C; gọi K là tâm đường tròn ngoại tiếp tam giác MDC. Chứng minh rằng hai đường tròn (I) và (K) cắt nhau.
Phương pháp giải - Xem chi tiết
a) Chứng minh 3 điểm I, D, J thẳng hàng và \(IJ = ID + DJ\) suy ra hai đường tròn (I) và (J) tiếp xúc ngoài với nhau tại D.
b) + Do (K) và (I) có điểm chung là D nên chúng chỉ có thể cắt nhau hoặc tiếp xúc nhau.
+ Chứng minh (K) tiếp xúc với (I) là vô lí. Suy ra (K) và (I) là hai đường tròn cắt nhau.
Lời giải chi tiết
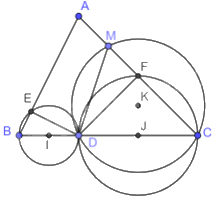
a) Tâm I của đường tròn ngoại tiếp tam giác vuông EBD là trung điểm của đoạn thẳng BD.
Tâm J của đường tròn ngoại tiếp tam giác vuông FDC là trung điểm của đoạn thẳng DC.
Vì D nằm trên BC nên ba điểm I, D, J thẳng hàng và \(IJ = ID + DJ\).
Suy ra, hai đường tròn (I) và (J) tiếp xúc ngoài với nhau tại D.
b) Do (K) và (I) có điểm chung là D nên chúng chỉ có thể cắt nhau hoặc tiếp xúc nhau.
Nếu (K) tiếp xúc với (I) thì D là tiếp điểm và K, I, D thẳng hàng, nghĩa là K thuộc đoạn DC và \(KD = KC\).
Vậy K phải trùng với trung điểm J của đoạn CD.
Điều đó nghĩa là đường tròn (K) trùng với đường tròn (J) và M trùng với F (trái với giả thiết).
Do đó, (K) và (I) là hai đường tròn cắt nhau.
Bài 12 trang 73 Sách bài tập Toán 9 - Kết nối tri thức tập 2 thuộc chương trình học về hàm số bậc nhất và hàm số bậc hai. Bài tập này thường yêu cầu học sinh xác định hệ số góc, đường thẳng song song, vuông góc, và ứng dụng vào giải quyết các bài toán liên quan đến thực tế.
Bài tập 12 trang 73 thường bao gồm các dạng bài sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào phân tích từng phần của bài tập.
Để xác định hệ số góc của đường thẳng, ta cần đưa phương trình đường thẳng về dạng y = ax + b, trong đó a là hệ số góc.
Ví dụ: Cho đường thẳng 2x + 3y = 6. Để xác định hệ số góc, ta biến đổi phương trình về dạng y = -2/3x + 2. Vậy hệ số góc của đường thẳng là -2/3.
Để tìm phương trình đường thẳng khi biết hệ số góc và một điểm thuộc đường thẳng, ta sử dụng công thức: y - y0 = a(x - x0), trong đó (x0, y0) là tọa độ của điểm thuộc đường thẳng.
Ví dụ: Tìm phương trình đường thẳng có hệ số góc là 2 và đi qua điểm A(1, 3). Ta có: y - 3 = 2(x - 1) => y = 2x + 1.
Để xác định mối quan hệ giữa hai đường thẳng y = a1x + b1 và y = a2x + b2, ta thực hiện như sau:
Khi giải bài toán thực tế, ta cần đọc kỹ đề bài, xác định các yếu tố liên quan đến hàm số và xây dựng phương trình toán học phù hợp. Sau đó, giải phương trình để tìm ra kết quả.
Bài 12 trang 73 Sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số. Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn khi giải bài tập này.
| Dạng bài | Phương pháp giải |
|---|---|
| Xác định hệ số góc | Đưa phương trình về dạng y = ax + b |
| Tìm phương trình đường thẳng | Sử dụng công thức y - y0 = a(x - x0) |
| Xác định mối quan hệ giữa hai đường thẳng | So sánh hệ số góc |