Bài 9.5 trang 51 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hệ phương trình bậc nhất hai ẩn để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hai điểm B, C nằm trên đường tròn (O) và cho điểm A nằm trên cung lớn $oversetfrown{BC}$. Biết rằng (widehat {OBA} = {30^o},widehat {OCA} = {40^o}). Tính số đo các góc của tam giác ABC.
Đề bài
Cho hai điểm B, C nằm trên đường tròn (O) và cho điểm A nằm trên cung lớn $\overset\frown{BC}$. Biết rằng \(\widehat {OBA} = {30^o},\widehat {OCA} = {40^o}\). Tính số đo các góc của tam giác ABC.
Phương pháp giải - Xem chi tiết
Trong một đường tròn, các góc nội tiếp chắn cung nhỏ thì có số đo bằng nửa số đo góc ở tâm chắn cùng một cung.
Lời giải chi tiết
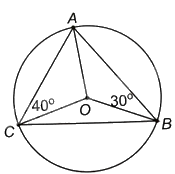
Tam giác OAB cân tại O (do \(OA = OB\)) nên \(\widehat {OAB} = \widehat {OBA} = {30^o}\).
Lại có: \(\widehat {OAB} + \widehat {OBA} + \widehat {AOB} = {180^o}\) nên \(\widehat {AOB} = {180^o} - \widehat {OAB} - \widehat {OBA} = {120^o}\).
Tam giác OAC cân tại O (do \(OA = OC\)) nên \(\widehat {OAC} = \widehat {OCA} = {40^o}\).
Lại có: \(\widehat {OAC} + \widehat {OCA} + \widehat {AOC} = {180^o}\) nên \(\widehat {AOC} = {180^o} - \widehat {OAC} - \widehat {OCA} = {100^o}\).
Xét đường tròn (O):
+ Góc nội tiếp ABC và góc ở tâm AOC cùng chắn cung nhỏ AC nên \(\widehat {ABC} = \frac{1}{2}\widehat {AOC} = {50^o}\).
+ Góc nội tiếp ACB và góc ở tâm AOB cùng chắn cung nhỏ AB nên \(\widehat {ACB} = \frac{1}{2}\widehat {AOB} = {60^o}\).
Tam giác ABC có: \(\widehat {CAB} + \widehat {ACB} + \widehat {CBA} = {180^o}\) nên \(\widehat {CAB} = {180^o} - \widehat {ABC} - \widehat {ACB} = {70^o}\).
Bài 9.5 trang 51 sách bài tập Toán 9 - Kết nối tri thức tập 2 thuộc chương trình học về hệ phương trình bậc nhất hai ẩn. Bài toán này thường xuất hiện trong các đề thi và kiểm tra, do đó việc nắm vững phương pháp giải là rất quan trọng.
(Nội dung đề bài sẽ được chèn vào đây. Ví dụ: Một người đi xe máy từ A đến B với vận tốc 40km/h. Nếu người đó tăng vận tốc thêm 5km/h thì sẽ đến B sớm hơn 18 phút. Tính quãng đường AB.)
Để giải bài toán này, chúng ta sẽ sử dụng phương pháp giải hệ phương trình bậc nhất hai ẩn. Các bước thực hiện như sau:
Xác định các đại lượng chưa biết trong bài toán và đặt ẩn số tương ứng. Ví dụ, trong bài toán trên, ta có thể đặt:
Dựa vào các mối quan hệ giữa các đại lượng đã cho trong bài toán, ta lập hệ phương trình. Ví dụ:
Sử dụng các phương pháp giải hệ phương trình bậc nhất hai ẩn (phương pháp thế, phương pháp cộng đại số) để tìm ra giá trị của các ẩn số.
Thay các giá trị tìm được vào bài toán để kiểm tra xem kết quả có hợp lý hay không.
(Lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước đặt ẩn, lập hệ phương trình, giải hệ phương trình và kiểm tra lại kết quả. Lời giải cần được trình bày rõ ràng, dễ hiểu, có giải thích chi tiết từng bước.)
Để củng cố kiến thức và kỹ năng giải bài toán hệ phương trình bậc nhất hai ẩn, các em có thể tham khảo các bài tập tương tự sau:
Khi giải bài toán hệ phương trình bậc nhất hai ẩn, các em cần lưu ý những điều sau:
Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin giải bài 9.5 trang 51 sách bài tập Toán 9 - Kết nối tri thức tập 2 và các bài tập tương tự. Chúc các em học tốt!