Bài 5.33 trang 72 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5.33 trang 72, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
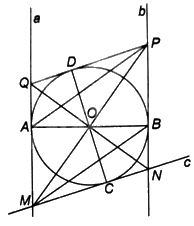
Cho đường tròn (O), đường thẳng a tiếp xúc với (O) tại A, đường thẳng b tiếp xúc với (O) tại B sao cho a//b. Gọi C là một điểm tùy ý thuộc (O), khác A và B. Tiếp tuyến c của (O) tại C cắt a và b lần lượt tại M và N. a) Chứng minh AB là một đường kính của (O). b) Gọi D, P và Q lần lượt là các điểm đối xứng với C, M và N qua tâm O. Chứng minh rằng (D in left( O right),P in b) và (Q in a). c) Chứng minh rằng PQ tiếp xúc với (O) tại D. d) Chứng minh tứ giác MNPQ là một hình thoi.
Đề bài
Cho đường tròn (O), đường thẳng a tiếp xúc với (O) tại A, đường thẳng b tiếp xúc với (O) tại B sao cho a//b. Gọi C là một điểm tùy ý thuộc (O), khác A và B. Tiếp tuyến c của (O) tại C cắt a và b lần lượt tại M và N.
a) Chứng minh AB là một đường kính của (O).
b) Gọi D, P và Q lần lượt là các điểm đối xứng với C, M và N qua tâm O. Chứng minh rằng \(D \in \left( O \right),P \in b\) và \(Q \in a\).
c) Chứng minh rằng PQ tiếp xúc với (O) tại D.
d) Chứng minh tứ giác MNPQ là một hình thoi.
Phương pháp giải - Xem chi tiết
a) + Chứng minh \(a \bot OA\), \(b \bot OB\) mà a//b nên ba điểm O, A, B thẳng hàng.
+ Lại có: \(OA = OB\) (bán kính của (O)). Do đó, AB là một đường kính của (O).
b) + Chứng minh D thuộc (O).
+ Chứng minh tứ giác AMBP là hình bình hành, suy ra BP//AM, suy ra BP//a. Mà b//a nên đường thẳng \(BP \equiv b\). Khi đó, P thuộc b.
+ Chứng minh tương tự ta có Q thuộc a.
c) + Chứng minh \(\Delta COM = \Delta DOP\left( {c.g.c} \right)\), suy ra \(\widehat {PDO} = \widehat {MCO} = {90^o}\).
+ Chứng minh \(\Delta CON = \Delta DOQ\left( {c.g.c} \right)\), suy ra \(\widehat {QDO} = \widehat {NCO} = {90^o}\).
+ Chứng minh \(\widehat {QDP} = {180^o}\). Suy ra, ba điểm P, D, Q thẳng hàng và PQ là tiếp tuyến của (O) tại D.
d) + Chứng minh tứ giác MNPQ là hình bình hành.
+ Chứng minh \(\widehat {AOM} = \widehat {MOC} = \frac{1}{2}\widehat {AOC}\), \(\widehat {BON} = \widehat {NOC} = \frac{1}{2}\widehat {BOC}\) nên \(\widehat {MOC} + \widehat {NOC} = {90^o}\) nên MP vuông góc với NQ tại O.
+ Hình bình hành MNPQ có đường chéo MP vuông góc với NQ tại O. Do đó, MNPQ là hình thoi.
Lời giải chi tiết
a) Vì a tiếp xúc với (O) tại A hay a là tiếp tuyến của (O) tại A. Do đó, \(a \bot OA\).
Vì b tiếp xúc với (O) tại B hay b là tiếp tuyến của (O) tại B. Do đó, \(b \bot OB\).
Lại có: a//b. Do đó, ba điểm O, A, B thẳng hàng.
Vì \(OA = OB\) nên AB là đường kính của (O).
b) Vì C thuộc (O) và D đối xứng với C qua O nên do tính đối xứng của đường tròn, suy ra D thuộc (O).
Tứ giác AMBP có: \(OA = OB\), \(OM = OP\) (P đối xứng với M qua O) nên tứ giác AMBP là hình bình hành, suy ra BP//AM. Vì M, A thuộc đường thẳng a nên BP//a.
Mà b//a nên đường thẳng \(BP \equiv b\). Khi đó, P thuộc b.
Chứng minh tương tự ta có Q thuộc a.
c) Tam giác COM và tam giác DOP có: \(OM = OP,OC = OD\) (vì D đối xứng với C qua O), \(\widehat {MOC} = \widehat {POD}\) (hai góc đối đỉnh) nên \(\Delta COM = \Delta DOP\left( {c.g.c} \right)\), suy ra \(\widehat {PDO} = \widehat {MCO} = {90^o}\).
Tương tự ta có: \(\Delta CON = \Delta DOQ\left( {c.g.c} \right)\), suy ra \(\widehat {QDO} = \widehat {NCO} = {90^o}\).
Ta có: \(\widehat {PDO} + \widehat {QDO} = \widehat {QDP} = {180^o}\) nên ba điểm P, D, Q thẳng hàng và PQ là tiếp tuyến của (O) tại D.
d) Tứ giác MNPQ có hai đường chéo MP và NQ cắt nhau tại trung điểm O của mỗi đường nên MNPQ là hình bình hành.
Vì MA và MC là hai tiếp tuyến cắt nhau tại M của (O) nên OM là tia phân giác của góc AOC.
Do đó, \(\widehat {AOM} = \widehat {MOC} = \frac{1}{2}\widehat {AOC}\).
Vì NB và NC là hai tiếp tuyến cắt nhau tại N của (O) nên ON là tia phân giác của góc BOC.
Do đó, \(\widehat {BON} = \widehat {NOC} = \frac{1}{2}\widehat {BOC}\).
Ta có:
\(\widehat {MOC} + \widehat {NOC} = \frac{1}{2}\left( {\widehat {AOC} + \widehat {BOC}} \right) \\= \frac{1}{2}{.180^o} = {90^o}.\)
Suy ra \(\widehat {MON} = {90^0}\) nên MP\( \bot \) NQ tại O.
Hình bình hành MNPQ có đường chéo MP vuông góc với NQ tại O.
Do đó, MNPQ là hình thoi.
Bài 5.33 thuộc chương Hàm số bậc nhất và hàm số bậc hai, sách bài tập Toán 9 - Kết nối tri thức tập 1. Để giải bài này, học sinh cần nắm vững các kiến thức sau:
Đề bài: (Đề bài cụ thể của bài 5.33 sẽ được trình bày ở đây. Ví dụ: Cho hàm số y = 2x - 3. Tìm giá trị của y khi x = 1.)
Lời giải:
Để hiểu rõ hơn về cách giải bài 5.33, chúng ta cùng xem xét một số ví dụ minh họa sau:
Ví dụ 1: (Đề bài ví dụ 1 và lời giải chi tiết)
Ví dụ 2: (Đề bài ví dụ 2 và lời giải chi tiết)
Ngoài ra, các em có thể tự giải các bài tập tương tự sau để củng cố kiến thức:
Khi giải các bài tập về hàm số, các em cần lưu ý những điều sau:
Bài 5.33 trang 72 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về hàm số. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em sẽ hiểu rõ phương pháp giải và tự tin làm bài tập.
| Dạng bài tập | Ví dụ | Phương pháp giải |
|---|---|---|
| Tìm giá trị của hàm số | y = 3x + 2, x = -1 | Thay x vào hàm số |
| Tìm điểm thuộc đồ thị hàm số | y = x2 - 4x + 3, y = 0 | Giải phương trình |
| Giải phương trình chứa hàm số | 2x + 5 = 0 | Biến đổi phương trình |