Bài 7.15 trang 31, 32 sách bài tập Toán 9 Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.15, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho bảng thống kê sau về số lượng học sinh tại một trường tham gia các câu lạc bộ (CLB): a) Lập các bảng tần số tương đối biểu diễn tỉ lệ học sinh nam, nữ tham gia các câu lạc bộ. b) Vẽ các biểu đồ hình quạt tròn biểu diễn các bảng tần số tương đối thu được ở câu a.
Đề bài
Cho bảng thống kê sau về số lượng học sinh tại một trường tham gia các câu lạc bộ (CLB):

a) Lập các bảng tần số tương đối biểu diễn tỉ lệ học sinh nam, nữ tham gia các câu lạc bộ.
b) Vẽ các biểu đồ hình quạt tròn biểu diễn các bảng tần số tương đối thu được ở câu a.
Phương pháp giải - Xem chi tiết
a) + Tính tần số tương đối ứng với các giá trị trong mẫu dữ liệu: Giá trị \({x_i}\) có tần số \({m_i}\) thì có tần số tương đối là: \({f_i} = \frac{{{m_i}}}{n}.100\left( \% \right)\) với m là tổng tất cả các tần số có trong mẫu số liệu.
+ Lập bảng tần số tương đối:
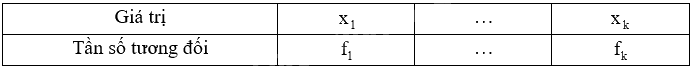
b) Cách vẽ biểu đồ hình quạt tròn biểu diễn bảng tần số tương đối:
Bước 1: Xác định số đo cung tương ứng của các hình quạt dùng để biểu diễn tần số tương đối của các giá trị theo công thức \({360^o}.{f_i}\) với \(i = 1,...,k\)
Bước 2: Vẽ hình tròn và chia hình tròn thành các hình quạt có số đo cung tương ứng được xác định trong Bước 1.
Bước 3: Định dạng các hình quạt tròn (thường bằng cách tô màu), ghi tần số tương đối, chú giải và tiêu đề.
Lời giải chi tiết
a) Với học sinh nam, tần số tương đối biểu diễn tỉ lệ tham gia CLB tiếng Anh, Toán, Khoa học lần lượt là:
\(\frac{{40}}{{150}}.100\% \approx 26,7\% ;\frac{{60}}{{150}}.100\% = 40\% ;\frac{{50}}{{150}}.100\% \approx 33,3\% \).
Bảng tần số tương đối:

Với học sinh nữ, tần số tương đối biểu diễn tỉ lệ tham gia CLB tiếng Anh, Toán, Khoa học lần lượt là: \(\frac{{70}}{{165}}.100\% \approx 42,4\% ;\frac{{30}}{{165}}.100\% \approx 18,2\% ;\frac{{65}}{{165}}.100\% \approx 39,4\% \).
Bảng tần số tương đối:

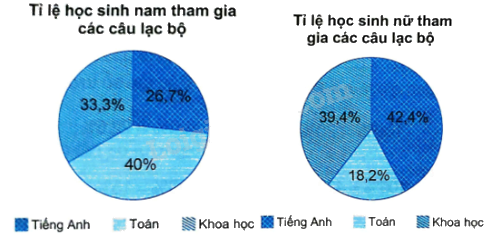
b) Biểu đồ hình quạt tròn:
Bài 7.15 sách bài tập Toán 9 Kết nối tri thức tập 2 yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến hàm số bậc nhất và hàm số bậc hai. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Dưới đây là lời giải chi tiết bài 7.15 trang 31, 32 sách bài tập Toán 9 Kết nối tri thức tập 2:
Để giải phần a, ta cần xác định hàm số biểu diễn mối quan hệ giữa hai đại lượng. Trong bài toán này, ta có thể xác định hàm số y = ax + b, trong đó y là giá trị tiền lương và x là số sản phẩm được làm ra.
Để tìm hệ số a và b, ta cần sử dụng các dữ kiện được cung cấp trong bài toán. Ví dụ, nếu ta biết rằng khi làm được 10 sản phẩm thì tiền lương là 500 nghìn đồng, và khi làm được 20 sản phẩm thì tiền lương là 1000 nghìn đồng, ta có thể lập hệ phương trình sau:
10a + b = 500
20a + b = 1000
Giải hệ phương trình này, ta sẽ tìm được giá trị của a và b, từ đó xác định được hàm số.
Sau khi đã xác định được hàm số, ta có thể sử dụng hàm số này để tính toán tiền lương khi làm được một số lượng sản phẩm khác. Ví dụ, nếu ta muốn tính tiền lương khi làm được 15 sản phẩm, ta chỉ cần thay x = 15 vào hàm số đã tìm được ở phần a.
Phần c của bài tập thường yêu cầu học sinh phân tích ý nghĩa của các hệ số trong hàm số. Ví dụ, hệ số a cho biết mức tăng tiền lương khi làm thêm một sản phẩm, và hệ số b cho biết tiền lương cố định.
Khi giải bài tập 7.15, học sinh cần chú ý các điểm sau:
Ngoài ra, học sinh có thể tham khảo các tài liệu học tập khác, chẳng hạn như sách giáo khoa, sách bài tập, và các trang web học toán online để nắm vững kiến thức và kỹ năng giải bài tập.
Hàm số là một công cụ toán học quan trọng được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống, chẳng hạn như kinh tế, tài chính, khoa học kỹ thuật, và y học. Việc nắm vững kiến thức về hàm số sẽ giúp học sinh hiểu rõ hơn về các hiện tượng thực tế và có khả năng giải quyết các bài toán thực tế một cách hiệu quả.
Ví dụ, trong lĩnh vực kinh tế, hàm số được sử dụng để mô tả mối quan hệ giữa cung và cầu, giữa chi phí và doanh thu, và giữa giá cả và số lượng hàng hóa. Trong lĩnh vực khoa học kỹ thuật, hàm số được sử dụng để mô tả các quá trình vật lý, hóa học, và sinh học. Trong lĩnh vực y học, hàm số được sử dụng để mô tả sự phát triển của bệnh tật và hiệu quả của các phương pháp điều trị.
Hy vọng rằng lời giải chi tiết bài 7.15 trang 31, 32 sách bài tập Toán 9 Kết nối tri thức tập 2 sẽ giúp các em học sinh học tập tốt hơn. Chúc các em thành công!