Bài 9.23 trang 55 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học Toán 9. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.23 trang 55, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho tứ giác ABCD nội tiếp đường tròn (O), hai đường chéo AC và BD cắt nhau tại điểm E. Tính số đo các góc của tứ giác ABCD, biết rằng (widehat {AEB} = {80^o},widehat {ABE} = {70^o}) và (widehat {ECB} = {50^o}).
Đề bài
Cho tứ giác ABCD nội tiếp đường tròn (O), hai đường chéo AC và BD cắt nhau tại điểm E. Tính số đo các góc của tứ giác ABCD, biết rằng \(\widehat {AEB} = {80^o},\widehat {ABE} = {70^o}\) và \(\widehat {ECB} = {50^o}\).
Phương pháp giải - Xem chi tiết
+ \(\widehat {BAE} = {180^o} - \widehat {AEB} - \widehat {ABE}\).
+ Ta có: \(\widehat {ACD} = \widehat {ABE} = {70^o}\),
\(\widehat {ADB} = \widehat {ECB} = {50^o}\),
\(\widehat {CDB} = \widehat {BAC} = {30^o}\).
+ \(\widehat {BCD} = \widehat {ECB} + \widehat {ACD} = {120^o},\)
\(\widehat {CDA} = \widehat {CDB} + \widehat {ADB} = {80^o}\).
+ Vì tứ giác ABCD nội tiếp đường tròn (O) nên \(\widehat {DAB} = {180^o} - \widehat {BCD},\widehat {ABC} = {180^o} - \widehat {CDA}\).
Lời giải chi tiết
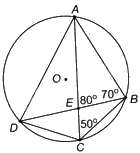
a) Tam giác ABE có: \(\widehat {BAE} = {180^o} - \widehat {AEB} - \widehat {ABE} = {30^o}\).
Xét đường tròn (O):
+ \(\widehat {ACD} = \widehat {ABE} = {70^o}\) (hai góc nội tiếp cùng chắn cung nhỏ AD).
+ \(\widehat {ADB} = \widehat {ECB} = {50^o}\) (hai góc nội tiếp cùng chắn cung nhỏ AB).
+ \(\widehat {CDB} = \widehat {BAC} = {30^o}\) (hai góc nội tiếp cùng chắn cung nhỏ CB).
Ta có:
\(\widehat {BCD} = \widehat {ECB} + \widehat {ACD} = {120^o},\\\widehat {CDA} = \widehat {CDB} + \widehat {ADB} = {80^o}.\)
Vì tứ giác ABCD nội tiếp đường tròn (O) nên
\(\widehat {DAB} = {180^o} - \widehat {BCD} = {60^o},\)
\(\widehat {ABC} = {180^o} - \widehat {CDA} = {100^o}.\)
Bài 9.23 sách bài tập Toán 9 - Kết nối tri thức tập 2 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc nhất và hàm số bậc hai. Để giải bài toán này, học sinh cần nắm vững các kiến thức sau:
Trước khi bắt đầu giải bài toán, học sinh cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 9.23, yêu cầu của bài toán là gì? Các dữ kiện nào được cho trong đề bài? Cần tìm gì?
Sau khi phân tích đề bài, học sinh cần xây dựng mô hình toán học để biểu diễn bài toán bằng ngôn ngữ toán học. Điều này có nghĩa là xác định các biến, các hàm số và các phương trình cần thiết để giải bài toán.
Sau khi xây dựng mô hình toán học, học sinh cần giải các phương trình để tìm nghiệm. Trong bài 9.23, có thể cần giải phương trình bậc nhất, phương trình bậc hai hoặc hệ phương trình.
Sau khi tìm được nghiệm, học sinh cần kiểm tra lại nghiệm để đảm bảo rằng nghiệm đó thỏa mãn điều kiện của bài toán. Nếu nghiệm thỏa mãn, học sinh có thể kết luận và trả lời câu hỏi của bài toán.
(Nội dung lời giải chi tiết bài 9.23 sẽ được trình bày tại đây, bao gồm các bước giải cụ thể, các phép tính và các giải thích rõ ràng. Lời giải sẽ được trình bày một cách logic và dễ hiểu, giúp học sinh nắm vững phương pháp giải bài toán.)
Ví dụ, nếu bài toán yêu cầu tìm phương trình đường thẳng đi qua hai điểm A(x1, y1) và B(x2, y2), lời giải sẽ bao gồm các bước sau:
Ngoài bài 9.23, còn rất nhiều bài tập tương tự trong sách bài tập Toán 9 - Kết nối tri thức tập 2. Để giải các bài tập này, học sinh có thể áp dụng các phương pháp giải tương tự như đã trình bày ở trên.
Một số dạng bài tập tương tự bao gồm:
Để nắm vững kiến thức về hàm số bậc nhất và hàm số bậc hai, học sinh cần luyện tập thêm nhiều bài tập khác nhau. Giaitoan.edu.vn cung cấp một kho bài tập phong phú, đa dạng, giúp học sinh rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi.
Hãy truy cập giaitoan.edu.vn để tìm thêm các bài giải chi tiết và bài tập luyện tập về Toán 9.
Bài 9.23 trang 55 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng, giúp học sinh củng cố kiến thức về hàm số bậc nhất và hàm số bậc hai. Hy vọng rằng với lời giải chi tiết và hướng dẫn giải bài tập mà giaitoan.edu.vn cung cấp, các em học sinh sẽ hiểu rõ phương pháp giải và tự tin làm bài tập.