Bài 5.18 trang 65 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5.18 trang 65, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho đường thẳng a, điểm M thuộc a và số dương R. Vẽ đường thẳng b đi qua M và vuông góc với a. Trên b xác định điểm A sao cho (AM = R) (đvđd). Chứng minh rằng đường tròn (A; R) tiếp xúc với a tại M. Ta có thể vẽ được mấy đường tròn như thế?
Đề bài
Cho đường thẳng a, điểm M thuộc a và số dương R.
Vẽ đường thẳng b đi qua M và vuông góc với a. Trên b xác định điểm A sao cho \(AM = R\) (đvđd). Chứng minh rằng đường tròn (A; R) tiếp xúc với a tại M. Ta có thể vẽ được mấy đường tròn như thế?
Phương pháp giải - Xem chi tiết
+ Vì M thuộc đường tròn (A; R) và \(a \bot AM\) tại M nên đường tròn (A; R) tiếp xúc với a tại M.
+ Vì có hai điểm thuộc đường thẳng b và cách M một khoảng bằng R nên có hai đường tròn thỏa mãn bài toán.
Lời giải chi tiết
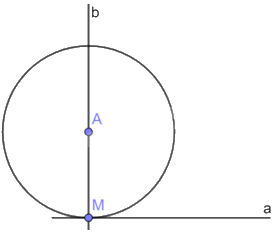
Vì M thuộc đường tròn (A; R) và \(a \bot AM\) tại M nên đường tròn (A; R) tiếp xúc với a tại M.
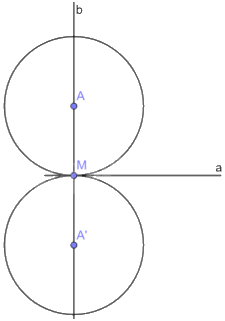
Vì có hai điểm (A và A’) thuộc đường thẳng b và cách M một khoảng bằng R nên có hai đường tròn thỏa mãn bài toán.
Bài 5.18 thuộc chương Hàm số bậc nhất và hàm số bậc hai, tập trung vào việc ứng dụng các kiến thức đã học để giải quyết các bài toán liên quan đến hàm số trong thực tế. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Đề bài: (Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho hàm số y = 2x + 3. Tìm giá trị của x khi y = 7.)
Lời giải:
Ngoài bài 5.18, còn rất nhiều bài tập tương tự trong sách bài tập Toán 9 - Kết nối tri thức tập 1. Các bài tập này thường yêu cầu học sinh:
Để giải quyết các bài tập này, học sinh cần:
Kiến thức về hàm số bậc nhất và hàm số bậc hai có ứng dụng rất lớn trong thực tế, đặc biệt trong các lĩnh vực như kinh tế, kỹ thuật, khoa học tự nhiên. Ví dụ, hàm số có thể được sử dụng để mô tả sự thay đổi của giá cả hàng hóa, tốc độ tăng trưởng dân số, hoặc quỹ đạo của một vật thể chuyển động.
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, các em học sinh có thể tự giải các bài tập sau:
Bài 5.18 trang 65 Sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và hàm số bậc hai. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài toán tương tự.