Bài 1.16 trang 19 SGK Toán 10 tập 1 thuộc chương 1: Mệnh đề và tập hợp, là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về mệnh đề, tập hợp và các phép toán trên tập hợp. Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cập nhật lời giải mới nhất và chính xác nhất, đồng thời cung cấp các bài tập luyện tập để các em có thể củng cố kiến thức đã học.
Để phục vụ cho một hội nghị quốc tế, ban tổ chức huy động 35 người phiên dịch tiếng Anh, 30 người phiên dịch tiếng Pháp, trong đó có 16 người phiên dịch được cả hai thứ tiếng Anh và Pháp. Hãy trả lời các câu hỏi sau: a) Ban tổ chức đã huy động bao nhiêu người phiên dịch cho hội nghị đó? b) Có bao nhiêu người chỉ phiên dịch được tiếng Anh? c) Có bao nhiêu người chỉ phiên dịch được tiếng Pháp?
Đề bài
Để phục vụ cho một hội nghị quốc tế, ban tổ chức huy động 35 người phiên dịch tiếng Anh, 30 người phiên dịch tiếng Pháp, trong đó có 16 người phiên dịch được cả hai thứ tiếng Anh và Pháp. Hãy trả lời các câu hỏi sau:
a) Ban tổ chức đã huy động bao nhiêu người phiên dịch cho hội nghị đó?
b) Có bao nhiêu người chỉ phiên dịch được tiếng Anh?
c) Có bao nhiêu người chỉ phiên dịch được tiếng Pháp?
Phương pháp giải - Xem chi tiết
Sử dụng biểu đồ Ven.
Lời giải chi tiết
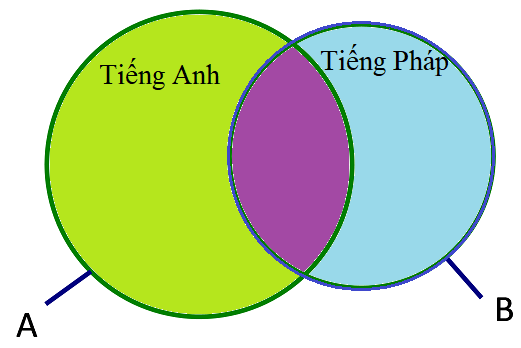
Gọi A là tập hợp những người phiên dịch tiếng Anh, B là tập hợp những người phiên dịch tiếng Pháp.
Ta có: \(n\left( A \right) = 35\), \(n\left( B \right) = 30\).
Biểu đồ Ven
a) \(n\;\left( {A \cup B} \right) = n\;(A) + n\;(B) - n\;(A \cap B) = 35 + 30 - 16 = 49\)
Vậy ban tổ chức đã huy động 49 người phiên dịch cho hội nghị đó
b) Có 35 người phiên dịch tiếng Anh, nhưng trong đó có 16 người phiên dịch được cả tiếng pháp, do đó số người chỉ phiên dịch được tiếng Anh là:
\(n\;\left( {A\,{\rm{\backslash }}\,B} \right) = n\;(A) - n\;(A \cap B) = 35 - 16 = 19\)
c) Có 30 người phiên dịch tiếng Pháp, nhưng trong đó có 16 người phiên dịch được cả tiếng Anh, do đó số người chỉ phiên dịch được tiếng Pháp là:
\(n\left( {B\,{\rm{\backslash }}\,{\rm{A}}} \right) = n\;(B) - n\;(B \cap A) = 30 - 16 = 14\)
Bài 1.16 yêu cầu chúng ta xác định tính đúng sai của các mệnh đề liên quan đến tập hợp. Để giải bài này, chúng ta cần nắm vững các khái niệm cơ bản về tập hợp, bao gồm:
Để giải bài 1.16, chúng ta sẽ xét từng mệnh đề một và sử dụng các định nghĩa trên để xác định tính đúng sai.
Mệnh đề: ∀x ∈ ℝ, x2 + 1 > 0
Phân tích: Mệnh đề này khẳng định rằng với mọi số thực x, x2 + 1 luôn lớn hơn 0. Vì x2 luôn lớn hơn hoặc bằng 0 với mọi x ∈ ℝ, nên x2 + 1 luôn lớn hơn 0. Do đó, mệnh đề này là đúng.
Mệnh đề: ∃x ∈ ℝ, x2 - 1 = 0
Phân tích: Mệnh đề này khẳng định rằng tồn tại một số thực x sao cho x2 - 1 = 0. Ta có thể giải phương trình x2 - 1 = 0 để tìm ra các giá trị của x thỏa mãn. Phương trình có nghiệm x = 1 và x = -1. Do đó, mệnh đề này là đúng.
Mệnh đề: ∀x ∈ ℝ, x + 1/x ≥ 2
Phân tích: Mệnh đề này khẳng định rằng với mọi số thực x, x + 1/x luôn lớn hơn hoặc bằng 2. Mệnh đề này không đúng với mọi x ∈ ℝ. Ví dụ, nếu x = -1, thì x + 1/x = -1 - 1 = -2, không thỏa mãn bất đẳng thức. Do đó, mệnh đề này là sai.
Mệnh đề: ∃x ∈ ℝ, x2 + 2x + 1 < 0
Phân tích: Mệnh đề này khẳng định rằng tồn tại một số thực x sao cho x2 + 2x + 1 < 0. Ta có thể viết lại biểu thức x2 + 2x + 1 thành (x + 1)2. Vì (x + 1)2 luôn lớn hơn hoặc bằng 0 với mọi x ∈ ℝ, nên (x + 1)2 không thể nhỏ hơn 0. Do đó, mệnh đề này là sai.
Để củng cố kiến thức về mệnh đề và tập hợp, các em có thể làm thêm các bài tập sau:
Bài 1.16 trang 19 SGK Toán 10 tập 1 – Kết nối tri thức là một bài tập quan trọng giúp học sinh làm quen với các khái niệm cơ bản về mệnh đề và tập hợp. Việc nắm vững kiến thức này sẽ là nền tảng vững chắc cho các bài học tiếp theo trong chương trình Toán 10.