Chào mừng bạn đến với bài học về Lý thuyết Đường tròn trong mặt phẳng tọa độ, một phần quan trọng trong chương trình SGK Toán 10 Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và cần thiết để hiểu rõ về đường tròn, phương trình đường tròn và các ứng dụng của nó trong giải toán.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn những bài giảng chất lượng, dễ hiểu và bài tập thực hành phong phú để giúp bạn nắm vững kiến thức một cách hiệu quả nhất.
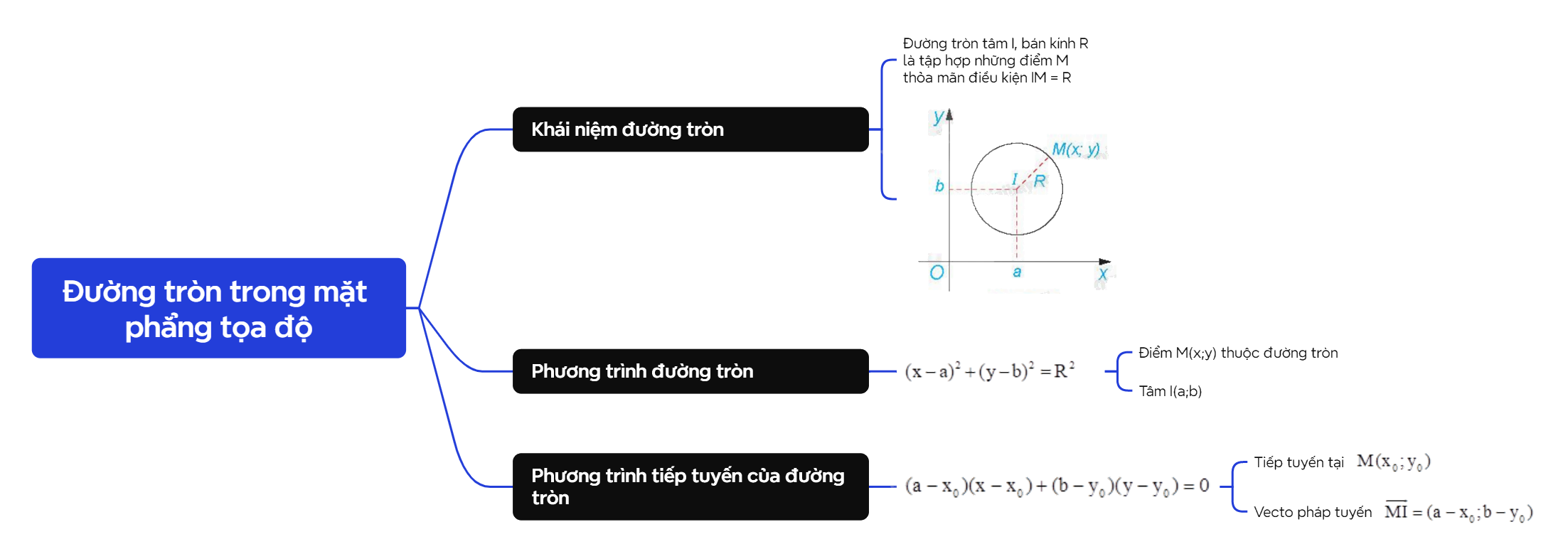
A. Lý thuyết 1. Phương trình đường tròn Đường tròn tâm I, bán kính R là tập hợp những điểm M thỏa mãn điều kiện IM = R. Do đó, để lập phương trình đường tròn, ta cần chuyển điều kiện hình học IM = R thành một điều kiện đại số.
A. Lý thuyết
1. Phương trình đường tròn
Đường tròn tâm I, bán kính R là tập hợp những điểm M thỏa mãn điều kiện IM = R. Do đó, để lập phương trình đường tròn, ta cần chuyển điều kiện hình học IM = R thành một điều kiện đại số.
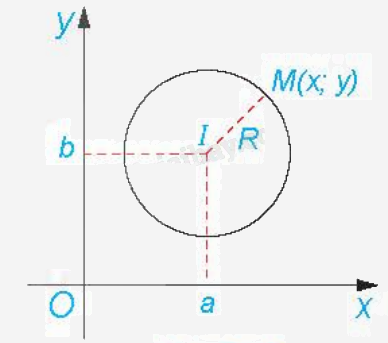
Điểm M(x;y) thuộc đường tròn (C), tâm I(a;b), bán kính R khi và chỉ khi \({(x - a)^2} + {(y - b)^2} = {R^2}\). Phương trình trên là phương trình đường tròn (C). |
Nhận xét: Phương trình \({x^2} + {y^2} - 2ax - 2by + c = 0\) là phương trình của một đường tròn (C) khi và chỉ khi \({a^2} + {b^2} - c > 0\). Khi đó, (C) có tâm I(a;b) và bán kính \(R = \sqrt {{a^2} + {b^2} - c} \).
2. Phương trình tiếp tuyến của đường tròn
Cho điểm \(M({x_0};{y_0})\) thuộc đường tròn (C): \({(x - a)^2} + {(y - b)^2} = {R^2}\) (tâm I(a;b), bán kính R). Khi đó, tiếp tuyến \(\Delta \) của (C) tại \(M({x_0};{y_0})\) có vecto pháp tuyến \(\overrightarrow {MI} = (a - {x_0};b - {y_0})\) và phương trình \((a - {x_0})(x - {x_0}) + (b - {y_0})(y - {y_0}) = 0\). |
B. Bài tập
Bài 1:
a) Tìm tâm và bán kính đường tròn (C) có phương trình: \({(x - 2)^2} + {(y + 3)^2} = 16\).
b) Viết phương trình đường tròn (C’) tâm J(2;-1) và có bán kính gấp đôi bán kính đường tròn (C).
Giải:
a) Ta viết phương trình của (C) ở dạng \({(x - 2)^2} + {(y - ( - 3))^2} = {4^2}\).
Vậy (C) có tâm I(2;-3) và bán kính R = 4.
b) Đường tròn (C’) có tâm J(2;-1) và bán kính R’ = 2R = 8 nên có phương trình:
\({(x - 2)^2} + {(y + 1)^2} = 64\).
Bài 2: Phương trình \({x^2} + {y^2} - 4x + 2y - 4 = 0\) có phải là phương trình đường tròn không? Nếu có, xác định tọa độ tâm và bán kính của đường tròn đó.
Giải:
Từ phương trình, ta có \(a = \frac{{ - 4}}{{ - 2}} = 2\); \(b = \frac{2}{{ - 2}} = - 1\); c = -4.
Suy ra \({a^2} + {b^2} - c = {2^2} + {( - 1)^2} - ( - 4) = 9 > 0\).
Vậy phương trình \({x^2} + {y^2} - 4x + 2y - 4 = 0\) là phương trình đường tròn tâm I(2;-1) và bán kính \(R = \sqrt 9 = 3\).
Bài 3: Lập phương trình đường tròn đi qua ba điểm A(-1;1), B(0;-2), C(0;2).
Giải:
Giả sử tâm của đường tròn là điểm I(a;b). Ta có \(IA = IB = IC \Leftrightarrow I{A^2} = I{B^2} = I{C^2}\).
Khi đó:
\(\left\{ \begin{array}{l}{( - 1 - a)^2} + {(1 - b)^2} = {(0 - a)^2} + {( - 2 - b)^2}\\{(0 - a)^2} + {( - 2 - b)^2} = {(0 - a)^2} + {(2 - b)^2}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{a^2} + {b^2} + 2a - 2b + 2 = {a^2} + {b^2} + 4b + 4\\{a^2} + {b^2} + 4b + 4 = {a^2} + {b^2} - 4b + 4\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}2a - 2b = 4b + 2\\b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\).
Đường tròn tâm I(1;0) bán kính \(R = IC = \sqrt {{a^2} + {b^2} - 4b + 4} = \sqrt 5 \).
Phương trình đường tròn là \({(x - 1)^2} + {(y - 0)^2} = {(\sqrt 5 )^2}\).
Vậy phương trình đường tròn là \({(x - 1)^2} + {y^2} = 5\).
Bài 4: Cho đường tròn (C) có phương trình \({(x + 1)^2} + {(y - 3)^2} = 5\). Điểm M(0;1) có thuộc đường tròn (C) hay không? Nếu có, hãy viết phương trình tiếp tuyến tại M của (C).
Giải:
Do \({(0 + 1)^2} + {(1 - 3)^2} = 5\), nên điểm M thuộc (C).
Đường tròn (C) có tâm là I(-1;3). Tiếp tuyến của (C) tại M(0;1) có vecto pháp tuyến \( - 1(x - 0) + 2(y - 1) = 0 \Leftrightarrow x - 2y + 2 = 0\).
Đường tròn là một trong những hình học cơ bản và quan trọng trong chương trình Toán học. Trong mặt phẳng tọa độ, đường tròn được biểu diễn bằng một phương trình cụ thể, và việc hiểu rõ phương trình này là chìa khóa để giải quyết nhiều bài toán liên quan.
Đường tròn là tập hợp tất cả các điểm trong mặt phẳng cách một điểm cố định (gọi là tâm) một khoảng không đổi (gọi là bán kính).
Phương trình tổng quát của đường tròn có tâm I(a; b) và bán kính R là:
(x - a)² + (y - b)² = R²
Trong đó:
Ngoài phương trình tổng quát, đường tròn còn có thể được biểu diễn bằng các dạng phương trình khác:
Phương trình x² + y² - 2ax - 2by + c = 0 là phương trình của một đường tròn khi và chỉ khi:
a² + b² - c > 0
Khi đó:
Xét điểm M(x₀; y₀) và đường tròn (x - a)² + (y - b)² = R²:
Xét đường thẳng Δ: Ax + By + C = 0 và đường tròn (x - a)² + (y - b)² = R²:
Tính khoảng cách d từ tâm I(a; b) đến đường thẳng Δ:
d = |Aa + Bb + C| / √(A² + B²)
Ví dụ 1: Xác định tâm và bán kính của đường tròn có phương trình: x² + y² - 4x + 6y - 3 = 0
Giải:
a = 2, b = -3, c = -3
a² + b² - c = 4 + 9 + 3 = 16 > 0
Vậy đây là phương trình của một đường tròn có:
Ví dụ 2: Viết phương trình đường tròn có tâm I(1; 2) và đi qua điểm M(3; 4).
Giải:
Bán kính R = IM = √((3-1)² + (4-2)²) = √(4 + 4) = √8
Phương trình đường tròn: (x - 1)² + (y - 2)² = 8
Lý thuyết đường tròn có nhiều ứng dụng trong thực tế, như:
Hy vọng bài học này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về Lý thuyết Đường tròn trong mặt phẳng tọa độ. Hãy luyện tập thêm nhiều bài tập để nắm vững kiến thức và áp dụng vào giải quyết các bài toán thực tế.