Quy tắc đếm là một trong những kiến thức cơ bản và quan trọng trong chương trình Toán 10 Kết nối tri thức. Nắm vững lý thuyết này sẽ giúp bạn giải quyết nhiều bài toán đếm một cách nhanh chóng và chính xác.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu về Lý thuyết Quy tắc đếm, cùng với các bài tập vận dụng đa dạng để bạn có thể luyện tập và củng cố kiến thức.
1. Quy tắc cộng và sơ đồ hình cây
A. Lý thuyết
1. Quy tắc cộng và sơ đồ hình cây
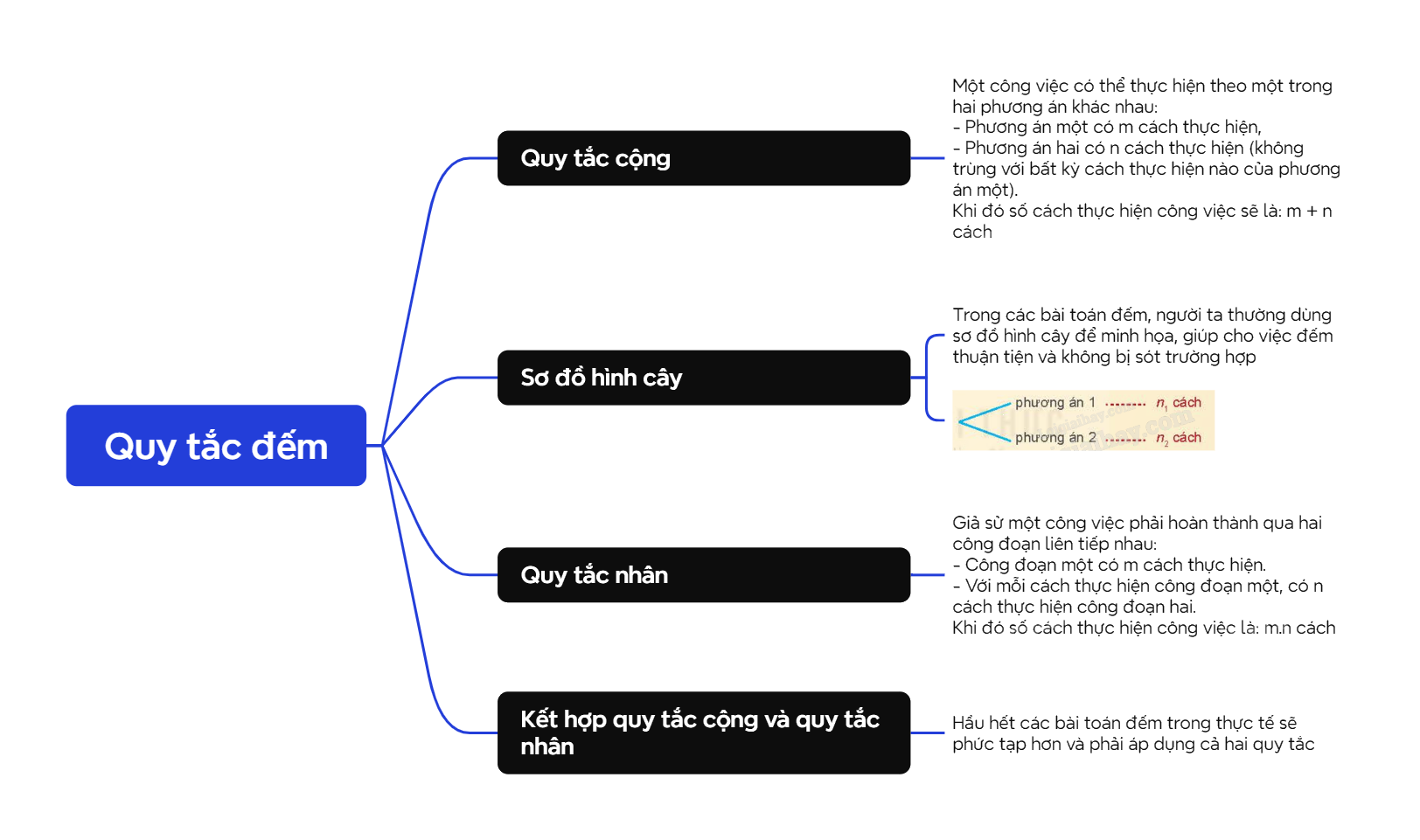
Giả sử một công việc có thể thực hiện theo một trong hai phương án khác nhau: - Phương án một có m cách thực hiện. - Phương án hai có n cách thực hiện (không trùng với bất kỳ cách thực hiện nào của phương án một). Khi đó số cách thực hiện công việc sẽ là: m + n cách. |

Chú ý: Sơ đồ minh họa cách phân chia trường hợp như trên được gọi là sơ đồ hình cây. Trong các bài toán đếm, người ta thường dùng sơ đồ hình cây để minh họa, giúp cho việc đếm thuận tiện và không bị sót trường hợp.
2. Quy tắc nhân
Giả sử một công việc phải hoàn thành qua hai công đoạn liên tiếp nhau: - Công đoạn một có m cách thực hiện. - Với mỗi cách thực hiện công đoạn một, có n cách thực hiện công đoạn hai. Khi đó số cách thực hiện công việc là: m.n cách. |
Chú ý: Quy tắc nhân áp dụng để tính số cách thực hiện một công việc có nhiều công đoạn, các công đoạn nối tiếp nhau và những công đoạn này độc lập với nhau.
3. Kết hợp quy tắc cộng và quy tắc nhân
Hầu hết các bài toán đếm trong thực tế sẽ phức tạp hơn và phải áp dụng cả hai quy tắc.
B. Bài tập
Bài 1: Bạn Phương có 7 quyển sách Tiếng Anh và 8 quyển sách Văn học, các quyển sách là khác nhau. Hỏi bạn Phương có bao nhiêu cách chọn một quyển sách để đọc?
Giải:
Việc chọn một quyển sách để đọc là thực hiện một trong hai hành động sau:
Chọn một quyển sách Tiếng Anh: Có 7 cách chọn.
Chọn một quyển sách Văn học: Có 8 cách chọn.
Vậy có 7 + 8 = 15 cách chọn một quyển sách để đọc.
Bài 2: Trong kinh doanh nhà hàng, combo là một hình thức gọi món theo thực đơn được kết hợp từ nhiều món ăn hoặc đồ uống. Nếu nhà hàng có 5 món rau, 4 món cá và 3 món thịt thì có bao nhiêu cách tạo ra một combo? Biết mỗi combo có đầy đủ 1 món rau, 1 món cá và 1 món thịt.
Giải:
Để tạo một combo, ta thực hiện ba hành động liên tiếp: chọn 1 món rau, chọn 1 món cá và chọn 1 món thịt.
Chọn 1 món rau: Có 5 cách chọn.
Chọn 1 món cá: Có 4 cách chọn.
Chọn 1 món thịt: Có 3 cách chọn.
Vậy có 5.4.3 = 60 cách tạo ra một combo.
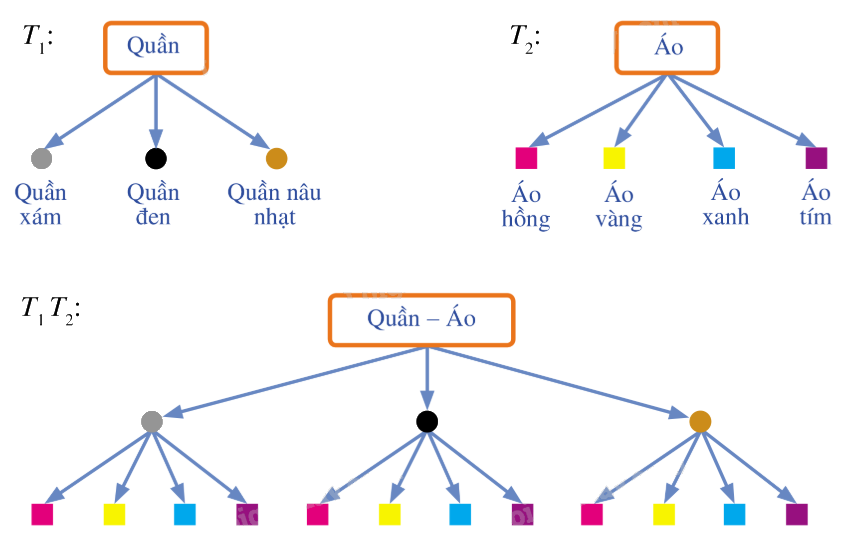
Bài 3: Bạn Hương có 3 chiếc quần khác màu: xám, đen, nâu nhạt và 4 chiếc áo sơ mi khác màu: hồng, vàng, xanh, tím. Hãy vẽ sơ đồ hình cây biểu thị số cách chọn:
a) 1 chiếc quần.
b) 1 chiếc áo sơ mi.
c) 1 bộ quần áo.
Giải:
Các sơ đồ hình cây \({T_1},{T_2},{T_1}{T_2}\) trong hình vẽ lần lượt:
a) Biểu thị số cách chọn 1 chiếc quần.
b) Biểu thị số cách chọn 1 chiếc áo sơ mi.
c) Biểu thị số cách chọn 1 bộ quần áo.
Bài 4: Cho 10 điểm phân biệt. Hỏi lập được bao nhiêu vectơ khác 0? Biết rằng hai đầu mút của mỗi vectơ là 2 trong 10 điểm đã cho.
Giải:
Việc lập vectơ là thực hiện hai hành động liên tiếp: chọn điểm đầu và chọn điểm cuối.
Chọn điểm đầu: Có 10 cách chọn. Chọn điểm cuối: Có 9 cách chọn. Theo quy tắc nhân, số vectơ lập được là: 10.9 = 90.
Bài 5: Đội văn nghệ của lớp 10B có 3 học sinh nữ và 2 học sinh nam. Giáo viên chủ nhiệm muốn chọn ra một đội tam ca gồm 3 học sinh sao cho có cả học sinh nam và học sinh nữ. Hỏi giáo viên chủ nhiệm có bao nhiêu cách chọn ra một đội tam ca như vậy?
Giải:
Khi chọn ra một đội tam ca gồm 3 học sinh có cả nam và nữ, giáo viên chủ nhiệm chỉ có thể chọn theo một trong hai khả năng.
* Xét khả năng thứ nhất: Chọn ra một học sinh nữ và hai học sinh nam.
- Có 3 cách chọn ra một học sinh nữ.
- Có 1 cách chọn ra hai học sinh nam.
Theo quy tắc nhân, số cách chọn ra một sinh nữ và hai học sinh nam là: 3.1 = 3.
* Xét khả năng thứ hai: Chọn ra hai học sinh nữ và một học sinh nam.
- Có 3 cách chọn ra hai học sinh nữ.
- Có 2 cách chọn ra một học sinh nam.
Theo quy tắc nhân, số cách chọn ra hai học sinh nữ và một học sinh nam là: 3.2 = 6.
Vậy theo tác cộng, số cách chọn ra một đội tam ca gồm 3 học sinh sao cho có cả học sinh nam và học sinh nữ cùng tham gia là: 3 + 6 = 9.
Bài 6: Cho kiểu gen AaBbDdEE. Giả sử quá trình giảm phân tạo giao tử bình thường, không xảy ra đột biến.
a) Vẽ sơ đồ hình cây biểu thị sự hình thành giao tử.
b) Từ đó, tính số loại giao tử của kiểu gen AaBbDdEE.
Giải:
a) Sơ đồ hình cây biểu thị sự hình thành giao tử:
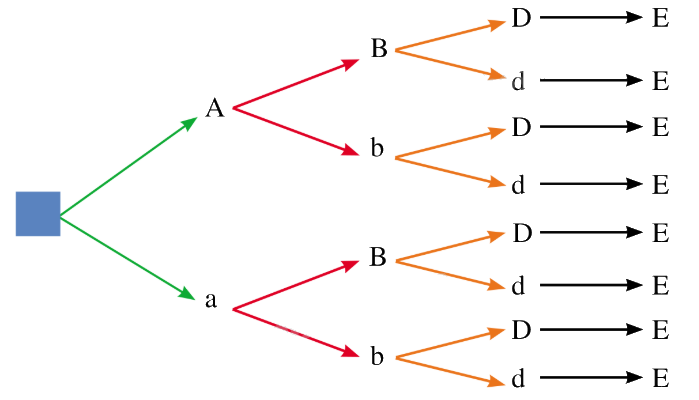
b) Từ sơ đồ hình cây, ta có 8 loại giao tử của kiểu gen AaBbDdEE.
Quy tắc đếm là một công cụ mạnh mẽ trong toán học, cho phép chúng ta tính số lượng các phần tử trong một tập hợp mà không cần liệt kê chúng một cách trực tiếp. Trong chương trình Toán 10 Kết nối tri thức, quy tắc đếm đóng vai trò quan trọng trong việc giải quyết các bài toán về tổ hợp, hoán vị và chỉnh hợp.
Trước khi đi sâu vào các quy tắc đếm, chúng ta cần nắm vững một số khái niệm cơ bản:
Quy tắc cộng được sử dụng khi có nhiều cách để thực hiện một hành động. Nếu có m cách để thực hiện hành động A và n cách để thực hiện hành động B, thì có m + n cách để thực hiện hoặc hành động A hoặc hành động B.
Ví dụ: Một học sinh có 3 chiếc áo sơ mi và 2 chiếc quần. Hỏi học sinh đó có bao nhiêu cách chọn một bộ quần áo?
Giải: Học sinh có 3 cách chọn áo sơ mi và 2 cách chọn quần. Vậy học sinh có 3 + 2 = 5 cách chọn một bộ quần áo.
Quy tắc nhân được sử dụng khi các hành động được thực hiện liên tiếp. Nếu có m cách để thực hiện hành động A và n cách để thực hiện hành động B, thì có m x n cách để thực hiện cả hai hành động A và B.
Ví dụ: Một người cần đi từ thành phố A đến thành phố B bằng ô tô. Có 2 con đường từ A đến B. Sau đó, người đó cần đi từ thành phố B đến thành phố C. Có 3 con đường từ B đến C. Hỏi người đó có bao nhiêu cách đi từ A đến C?
Giải: Người đó có 2 cách đi từ A đến B và 3 cách đi từ B đến C. Vậy người đó có 2 x 3 = 6 cách đi từ A đến C.
Hoán vị là một cách sắp xếp các phần tử của một tập hợp theo một thứ tự nhất định. Số hoán vị của n phần tử là n! (n giai thừa), được tính bằng công thức: n! = n x (n-1) x (n-2) x ... x 2 x 1.
Ví dụ: Có bao nhiêu cách sắp xếp 3 cuốn sách khác nhau trên một kệ sách?
Giải: Số hoán vị của 3 cuốn sách là 3! = 3 x 2 x 1 = 6.
Tổ hợp là một cách chọn một số phần tử từ một tập hợp mà không quan tâm đến thứ tự. Số tổ hợp chập k của n phần tử là Cnk, được tính bằng công thức: Cnk = n! / (k! x (n-k)!)
Ví dụ: Có bao nhiêu cách chọn 2 học sinh từ một lớp có 10 học sinh?
Giải: Số tổ hợp chập 2 của 10 học sinh là C102 = 10! / (2! x 8!) = 45.
Chỉnh hợp là một cách chọn một số phần tử từ một tập hợp và sắp xếp chúng theo một thứ tự nhất định. Số chỉnh hợp chập k của n phần tử là Ank, được tính bằng công thức: Ank = n! / (n-k)!
Ví dụ: Có bao nhiêu cách chọn và sắp xếp 2 học sinh từ một lớp có 10 học sinh để làm ban cán sự lớp (gồm lớp trưởng và lớp phó)?
Giải: Số chỉnh hợp chập 2 của 10 học sinh là A102 = 10! / 8! = 90.
Để hiểu rõ hơn về Lý thuyết Quy tắc đếm, bạn có thể thực hành các bài tập sau:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về Lý thuyết Quy tắc đếm - SGK Toán 10 Kết nối tri thức. Chúc bạn học tập tốt!