Bài 4.14 trang 58 SGK Toán 10 tập 1 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng của vectơ trong hình học. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.14 trang 58 SGK Toán 10 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy cùng theo dõi lời giải chi tiết dưới đây!
Cho tam giác ABC a) Hãy xác định điểm M để MA +MB+2MC=0 b) Chứng minh rằng với mọi điểm O, ta có OA+OB+2OC = 4OM
Đề bài
Cho tam giác ABC
a) Hãy xác định điểm M để \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \)
b) Chứng minh rằng với mọi điểm O, ta có \(\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = 4\overrightarrow {OM} \)
Phương pháp giải - Xem chi tiết
Với ba điểm A, B, C bất kì ta luôn có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Lời giải chi tiết
a) Ta có: \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {MA} + \left( {\overrightarrow {MA} + \overrightarrow {AB} } \right) + 2\left( {\overrightarrow {MA} + \overrightarrow {AC} } \right) = \overrightarrow 0 \)
\(\begin{array}{l} \Leftrightarrow 4\overrightarrow {MA} + \overrightarrow {AB} + 2\overrightarrow {AC} = \overrightarrow 0 \\ \Leftrightarrow 4\overrightarrow {AM} = \overrightarrow {AB} + 2\overrightarrow {AC} \\ \Leftrightarrow \overrightarrow {AM} = \frac{1}{4}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} \end{array}\)
Trên cạnh AB, AC lấy điểm D, E sao cho \(AD = \frac{1}{4}AB;\;\,AE = \frac{1}{2}AC\)
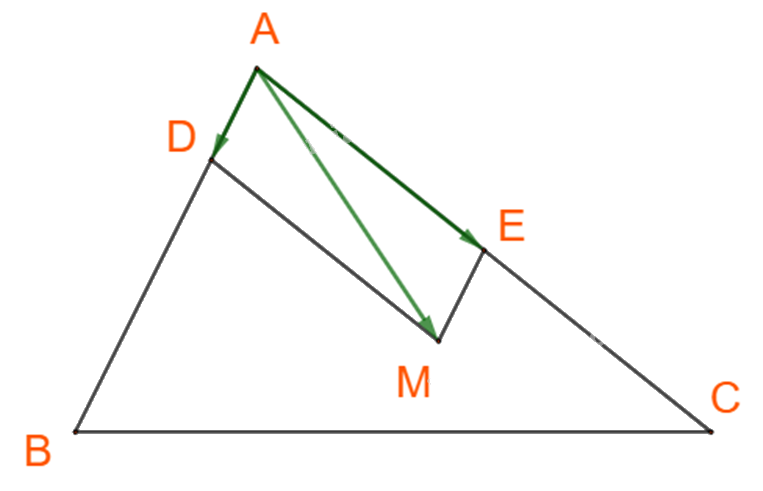
Khi đó \(\overrightarrow {AM} = \overrightarrow {AD} + \overrightarrow {AE} \) hay M là đỉnh thứ tư của hình bình hành AEMD.
Cách 2:
Ta có: \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \left( {\overrightarrow {MC} + \overrightarrow {CA} } \right) + \left( {\overrightarrow {MC} + \overrightarrow {CB} } \right) + 2\overrightarrow {MC} = \overrightarrow 0 \)
\(\begin{array}{l} \Leftrightarrow 4\overrightarrow {MC} + \overrightarrow {CA} + \overrightarrow {CB} = \overrightarrow 0 \\ \Leftrightarrow 4.\overrightarrow {CM} = \overrightarrow {CA} + \overrightarrow {CB} \end{array}\)
Gọi D là đỉnh thứ tư của hình bình hành ACBD.
Khi đó: \(\overrightarrow {CD} = \overrightarrow {CA} + \overrightarrow {CB} \)\( \Rightarrow 4.\overrightarrow {CM} = \overrightarrow {CD} \)
\( \Leftrightarrow \overrightarrow {CM} = \frac{1}{4}\overrightarrow {CD} \Leftrightarrow \overrightarrow {CM} = \frac{1}{2}\overrightarrow {CO} \)
Với O là tâm hình bình hành ACBD, cũng là trung điểm đoạn AB.
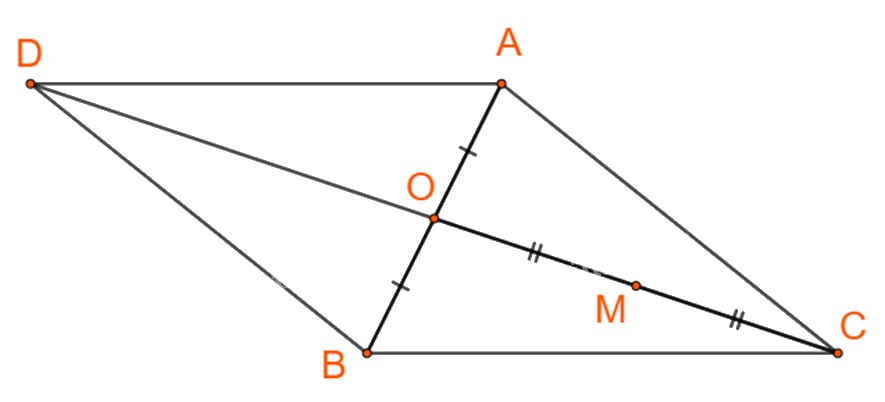
Vậy M là trung điểm của trung tuyến kẻ từ C của tam giác ABC.
b) Chứng minh rằng với mọi điểm O, ta có \(\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = 4\overrightarrow {OM} \)
Với mọi điểm O, ta có: \(\left\{ \begin{array}{l}\overrightarrow {OA} = \overrightarrow {OM} + \overrightarrow {MA} ;\;\\\overrightarrow {OB} = \overrightarrow {OM} + \overrightarrow {MB} ;\;\,\\\overrightarrow {OC} = \overrightarrow {OM} + \overrightarrow {MC} \end{array} \right.\)
\(\begin{array}{l} \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = \left( {\overrightarrow {OM} + \overrightarrow {MA} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {MB} } \right) + 2\left( {\overrightarrow {OM} + \overrightarrow {MC} } \right)\\ = 4\overrightarrow {OM} + \left( {\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} } \right) = 4\overrightarrow {OM} + \overrightarrow 0 = 4\overrightarrow {OM} .\end{array}\)
Vậy với mọi điểm O, ta có \(\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = 4\overrightarrow {OM} \).
Bài 4.14 trang 58 SGK Toán 10 tập 1 – Kết nối tri thức là một bài toán ứng dụng thực tế về vectơ, đòi hỏi học sinh phải hiểu rõ các khái niệm về vectơ, phép cộng, trừ vectơ, tích của một số với vectơ và các tính chất của chúng. Để giải bài toán này một cách hiệu quả, chúng ta cần phân tích đề bài, xác định các vectơ liên quan và sử dụng các công thức, định lý đã học để tìm ra lời giải.
Trước khi bắt đầu giải bài toán, chúng ta cần đọc kỹ đề bài và xác định rõ các yếu tố quan trọng. Trong bài 4.14, đề bài thường mô tả một tình huống thực tế liên quan đến các vật thể chuyển động hoặc các lực tác động. Chúng ta cần xác định các vectơ đại diện cho các yếu tố này, chẳng hạn như vectơ vận tốc, vectơ lực, vectơ dịch chuyển,…
Ví dụ, nếu đề bài mô tả một vật thể chuyển động với vận tốc v và gia tốc a, thì chúng ta có thể biểu diễn vận tốc và gia tốc bằng các vectơ v và a. Tương tự, nếu đề bài mô tả một lực F tác động lên một vật thể, thì chúng ta có thể biểu diễn lực này bằng vectơ F.
Sau khi đã xác định được các vectơ liên quan, chúng ta cần sử dụng các công thức và định lý đã học để giải bài toán. Một số công thức và định lý thường được sử dụng trong các bài toán về vectơ bao gồm:
Chúng ta cần lựa chọn các công thức và định lý phù hợp với từng bài toán cụ thể và áp dụng chúng một cách chính xác để tìm ra lời giải.
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 4.14 trang 58 SGK Toán 10 tập 1, chúng ta sẽ cùng xem xét một ví dụ minh họa cụ thể. (Nội dung ví dụ sẽ được trình bày chi tiết với các bước giải cụ thể, hình vẽ minh họa nếu cần thiết.)
Bước 1: Phân tích đề bài và xác định các vectơ liên quan.
Bước 2: Sử dụng các công thức và định lý liên quan để thiết lập các phương trình.
Bước 3: Giải các phương trình để tìm ra các giá trị cần tìm.
Bước 4: Kiểm tra lại kết quả và đưa ra kết luận.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài 4.14 trang 58 SGK Toán 10 tập 1 – Kết nối tri thức và các bài tập tương tự. Chúc các em học tập tốt!
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.