Chào mừng bạn đến với chuyên mục Lý thuyết Hàm số - SGK Toán 10 Kết nối tri thức tại giaitoan.edu.vn! Hàm số là một trong những khái niệm cơ bản và quan trọng nhất trong chương trình Toán học, đặc biệt là ở cấp THPT. Việc nắm vững lý thuyết hàm số sẽ giúp bạn giải quyết các bài toán một cách hiệu quả và xây dựng nền tảng vững chắc cho các kiến thức nâng cao.
Tại đây, chúng tôi cung cấp đầy đủ và chi tiết lý thuyết về hàm số, bao gồm định nghĩa, các loại hàm số, tính chất, và các phương pháp xét tính đơn điệu, cực trị của hàm số.
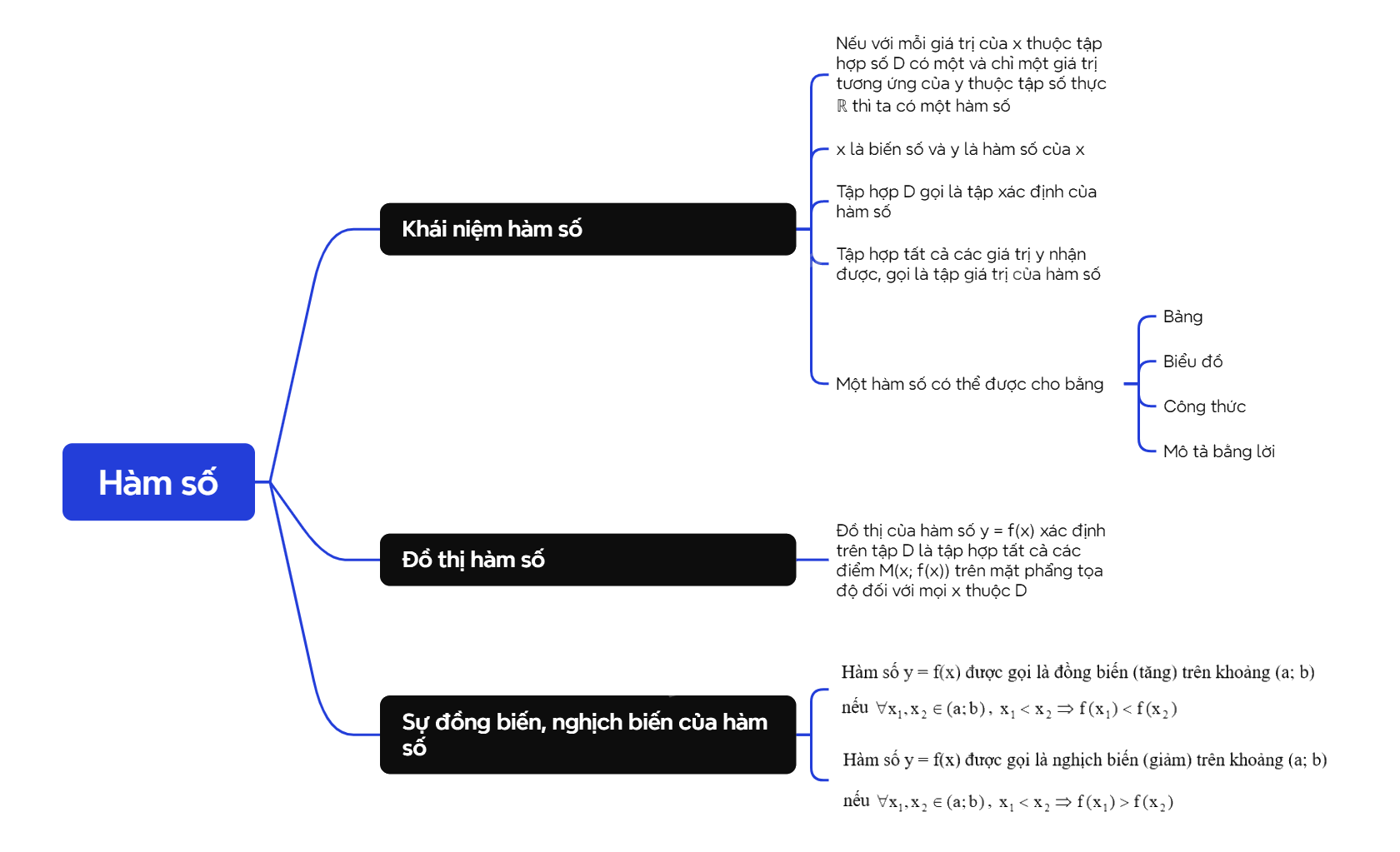
A. Lý thuyết 1. Khái niệm hàm số
A. Lý thuyết
1. Khái niệm hàm số
Nếu với mỗi giá trị của x thuộc tập hợp số D có một và chỉ một giá trị tương ứng của y thuộc tập số thực ℝ thì ta có một hàm số. Ta gọi x là biến số và y là hàm số của x. Tập hợp D gọi là tập xác định của hàm số. Tập hợp tất cả các giá trị y nhận được, gọi là tập giá trị của hàm số. |
Khi y là hàm số của x, ta có thể viết y = f(x), y = g(x),…
Chú ý: Khi cho hàm số bằng công thức y = f(x) mà không chỉ rõ tập xác định của nó thì ta quy ước tập xác định của hàm số là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.
Nhận xét: Một hàm số có thể được cho bằng bảng, bằng biểu đồ, bằng công thức hoặc mô tả bằng lời.
2. Đồ thị của hàm số
| Đồ thị của hàm số y = f(x) xác định trên tập D là tập hợp tất cả các điểm M(x; f(x)) trên mặt phẳng tọa độ đối với mọi x thuộc D. |
3. Sự đồng biến, nghịch biến của hàm số
Hàm số y = f(x) được gọi là đồng biến (tăng) trên khoảng (a; b), nếu \(\forall {x_1},{x_2} \in (a;b)\), \({x_1} < {x_2}\)\( \Rightarrow f({x_1}) < f({x_2})\). Hàm số y = f(x) được gọi là nghịch biến (giảm) trên khoảng (a; b), nếu \(\forall {x_1},{x_2} \in (a;b)\), \({x_1} < {x_2}\)\( \Rightarrow f({x_1}) > f({x_2})\). |
Chú ý:
- Đồ thị của một hàm số đồng biến trên khoảng (a; b) là đường “đi lên” từ trái sang phải.
- Đồ thị của một hàm số nghịch biến trên khoảng (a; b) là đường “đi xuống” từ trái sang phải.
B. Bài tập
Bài 1 (ví dụ): Bảng dưới đây cho biết nồng độ bụi PM 2.5 trong không khí theo thời gian trong ngày 25-3-2021 tại một trạm quan trắc ở Thủ đô Hà Nội:

Nếu gọi x là thời điểm, y là nồng độ bụi PM 2.5 thì x là biến số và y là hàm số của x. Đó là hàm số được cho bằng bảng. Tập xác định của hàm số là D = {0; 4; 8; 12; 16}. Tập giá trị của hàm số là {74,27; 64,58; 57,9; 69,07; 81,78}.
Bài 2: Viết hàm số mô tả sự phụ thuộc của quãng đường đi được vào thời gian của một vật chuyển động thẳng đều với vận tốc 2 m/s. Tìm tập xác định của hàm số đó. Tính quãng đường vật đi được sau 5 s, 10 s.
Giải:
Một vật chuyển động thẳng đều với vận tốc v = 2 m/s thì quãng đường đi được S phụ thuộc vào thời gian t (giây) theo công thức S = 2t, trong đó t là biến số, S là hàm số của t. Tập xác định của hàm số là D = [0; +∞). Quãng đường vật đi được sau 5 s: \({S_1} = S(5) = 2.5 = 10\) (m). Quãng đường vật đi được sau 10 s: \({S_2} = S(10) = 2.10 = 20\) (m).
Bài 3: Tìm tập xác định của các hàm số sau:
a) \(y = \sqrt {2x - 4} \).
b) \(y = \frac{1}{{x - 1}}\).
Giải:
a) Biểu thức \(\sqrt {2x - 4} \) có nghĩa khi \(2x - 4 \ge 0\), tức là khi \(x \ge 2\).
Vậy tập xác định của hàm số đã cho là \(D = [2; + \infty )\).
b) Biểu thức \(\frac{1}{{x - 1}}\) có nghĩa khi \(x - 1 \ne 0\), tức là khi \(x \ne 1\).
Vậy tập xác định của hàm số đã cho là \(D = \mathbb{R}\backslash \{ 1\} \).
Bài 4:
a) Cho hàm số \(y = f(x) = \frac{1}{8}{x^2}\) xác định trên D = [-3;5] có đồ thị (C) như hình.
- Điểm A(4; f(4)) có thuộc đồ thị (C) không?
- Lấy điểm B tùy ý trên đồ thị (C). Nêu nhận xét về hoành độ của điểm B.
b) Vẽ đồ thị hàm số y = f(x) được cho bởi bảng sau:
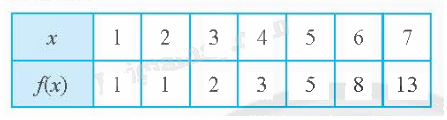
Giải:
a) Vì \(4 \in [ - 3;5]\) nên điểm A có hoành độ bằng 4 và tung độ \(y = \frac{1}{8}{.4^2} = 2\) là điểm thuộc đồ thị (C).
Khi lấy điểm B tùy ý trên đồ thị (C) thì hoành độ
\({x_B}\) của điểm này thuộc tập xác định D, nghĩa là \( - 3 \le {x_B} \le 5\).
b) Đồ thị hàm số gồm 7 điểm như hình:
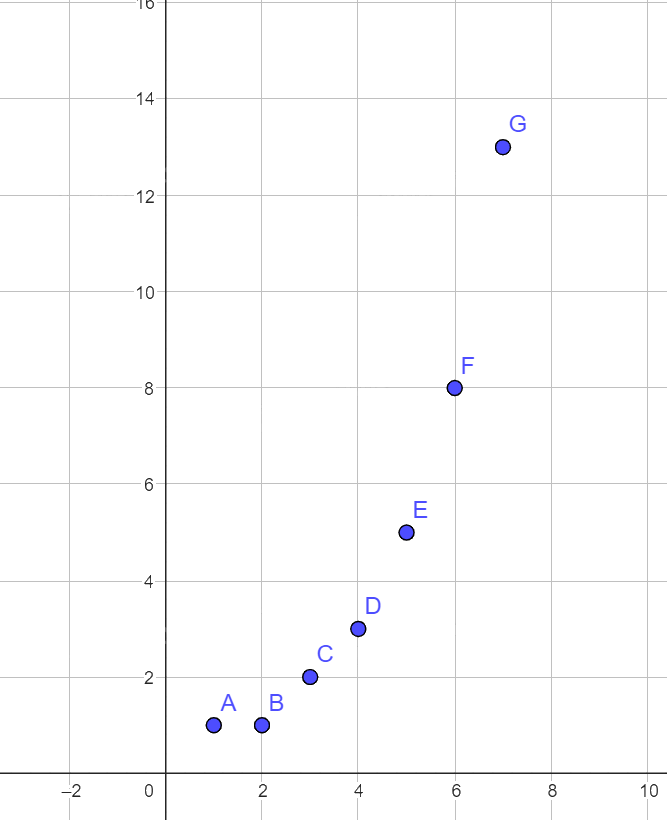
Bài 5: Hàm số \(y = {x^2}\) đồng biến hay nghịch biến trên mỗi khoảng \(( - \infty ;0)\) và \((0; + \infty )\)?
Giải:
Vẽ đồ thị hàm số \(y = f(x) = {x^2}\) như hình:
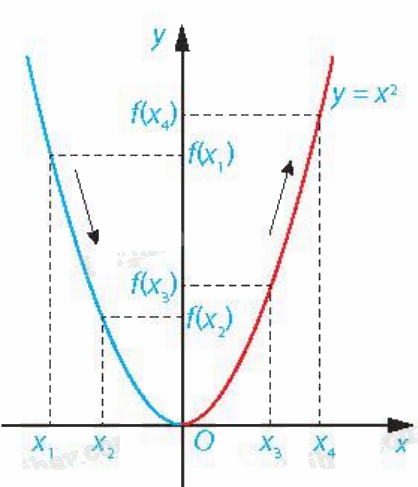
- Trên khoảng \(( - \infty ;0)\), đồ thị “đi xuống” từ trái sang phải và với \({x_1},{x_2} \in ( - \infty ;0)\), \({x_1} < {x_2}\) thì \(f({x_1}) > f({x_2})\).
Như vậy, hàm số \(y = {x^2}\) nghịch biến trên khoảng \(( - \infty ;0)\).
- Trên khoảng \((0; + \infty )\), đồ thị “đi lên” từ trái sang phải và với \({x_3},{x_4} \in (0; + \infty )\), \({x_3} < {x_4}\) thì \(f({x_3}) < f({x_4})\).
Như vậy, hàm số \(y = {x^2}\) đồng biến trên khoảng \((0; + \infty )\).
Hàm số là một quy tắc quan hệ giữa hai tập hợp, gán mỗi phần tử của tập hợp đầu vào (tập xác định) với một phần tử duy nhất của tập hợp đầu ra (tập giá trị). Trong chương trình Toán 10 Kết nối tri thức, học sinh bắt đầu làm quen với khái niệm hàm số thông qua các hàm số đơn giản như hàm số bậc nhất, hàm số bậc hai.
Một hàm số f từ tập hợp A (tập xác định) vào tập hợp B (tập giá trị) là một quy tắc tương ứng mỗi phần tử x thuộc A với một và chỉ một phần tử y thuộc B, ký hiệu là y = f(x).
Tập xác định (TXĐ) của hàm số là tập hợp tất cả các giá trị của x mà hàm số có nghĩa. Ví dụ, với hàm số y = 1/x, TXĐ là tất cả các số thực khác 0.
Tập giá trị (TGT) của hàm số là tập hợp tất cả các giá trị của y mà hàm số có thể nhận được. Ví dụ, với hàm số y = x2, TGT là tất cả các số thực không âm.
Hàm số bậc nhất y = ax + b:
Đồ thị hàm số là tập hợp tất cả các điểm có tọa độ (x, y) thỏa mãn phương trình y = f(x). Việc vẽ đồ thị hàm số giúp chúng ta hình dung được tính chất của hàm số một cách trực quan.
Bài 1: Xác định tập xác định của hàm số y = √(x - 2).
Giải: Hàm số có nghĩa khi x - 2 ≥ 0, tức là x ≥ 2. Vậy TXĐ của hàm số là [2, +∞).
Bài 2: Hàm số y = -2x + 3 có phải là hàm số đồng biến hay nghịch biến?
Giải: Vì a = -2 < 0, hàm số nghịch biến trên ℝ.
Hàm số có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và khoa học, như:
Để nắm vững kiến thức về hàm số, bạn nên luyện tập thường xuyên các bài tập khác nhau. Giaitoan.edu.vn cung cấp một hệ thống bài tập phong phú và đa dạng, giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán.
Lý thuyết hàm số là một phần quan trọng của chương trình Toán 10. Việc hiểu rõ các khái niệm, tính chất và ứng dụng của hàm số sẽ giúp bạn học tốt môn Toán và có nền tảng vững chắc cho các môn học khác. Chúc bạn học tập hiệu quả!