Giải bài 5.24 trang 90 SGK Toán 10 – Kết nối tri thức

Bài 5.24 trang 90 SGK Toán 10 – Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5.24 trang 90 SGK Toán 10 – Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập.

Bảng sau cho biết dân số của các tỉnh/thành phố Đồng bằng Bắc Bộ năm 2018 (đơn vị triệu người) a) Tìm số trung bình và trung vị của mẫu số liệu trên. b) Giải thích tại sao số trung bình và trung vị lại có sự sai khác nhiều. c) Nên sử dụng số trung bình hay trung vị để đại diện cho dân số của các tỉnh thuộc Đồng bằng Bắc Bộ?

Đề bài

Bảng sau cho biết dân số của các tỉnh/thành phố Đồng bằng Bắc Bộ năm 2018 (đơn vị triệu người)

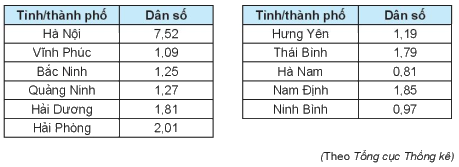
Giải bài 5.24 trang 90 SGK Toán 10 – Kết nối tri thức 1

a) Tìm số trung bình và trung vị của mẫu số liệu trên.

b) Giải thích tại sao số trung bình và trung vị lại có sự sai khác nhiều.

c) Nên sử dụng số trung bình hay trung vị để đại diện cho dân số của các tỉnh thuộc Đồng bằng Bắc Bộ?

Phương pháp giải - Xem chi tiết Giải bài 5.24 trang 90 SGK Toán 10 – Kết nối tri thức 2

- Sắp xếp lại mẫu số liệu theo thứ tự không giảm.

- Áp dụng công thức số trung bình của mẫu số liệu \({x_1},{x_2},...,{x_n}\):

\(\overline X = \frac{{{x_1} + {x_2} + ... + {x_n}}}{n}\)

- Số trung vị

+ Sắp xếp lại số liệu theo thứ tự không giảm.

+ Nếu số giá trị của mẫu số liệu là số lẻ thì giá trị chính giữa của mẫu là trung vị. Nếu là số chẵn thì trung vị là trung bình cộng của hai giá trị chính giữa của mẫu.

b) Trong trường hợp mẫu số liệu có giá trị bất thường (rất lớn hoặc rất bé so với đa số các giá trị khác) thì sẽ làm cho số trung bình và trung vị có sự khác nhau rõ rệt.

c) Trong trường hợp mẫu số liệu có giá trị bất thường (rất lớn hoặc rất bé so với đa số các giá trị khác), người ta không dùng số trung bình để đo xu thế trung tâm mà dùng trung vị.

Lời giải chi tiết

Sắp xếp lại:

0,81

0,97

1,09

1,19

1,25

1,27

1,79

1,81

1,85

2,01

7,52

Số trung bình Có 11 tỉnh thành nên n=11.

\(\begin{array}{l}\overline X = \frac{{7,52 + ... + 1,19 + ... + 0,97}}{{11}}\\ = 1,96\end{array}\)

Trung vị: 1,27

b) Ta thấy 7,52 lệch hẳn so với giá trị trung bình nên đây là giá trị bất thường của mẫu số liệu

=> Số trung bình và trung vị lại có sự sai khác nhiều

c) Nên sử dụng trung vị để đại diện cho dân số của các tỉnh thuộc Đồng bằng Bắc Bộ.

Xây dựng nền tảng Toán THPT vững vàng từ hôm nay! Đừng bỏ lỡ Giải bài 5.24 trang 90 SGK Toán 10 – Kết nối tri thức đặc sắc thuộc chuyên mục giải toán 10 trên nền tảng toán. Với bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát chương trình Toán lớp 10, đây chính là "kim chỉ nam" giúp các em tối ưu hóa ôn luyện, củng cố kiến thức cốt lõi và chuẩn bị hành trang vững chắc cho tương lai. Phương pháp học trực quan, logic sẽ mang lại hiệu quả vượt trội trên lộ trình chinh phục đại học!

Giải bài 5.24 trang 90 SGK Toán 10 – Kết nối tri thức: Hướng dẫn chi tiết và dễ hiểu

Bài 5.24 trang 90 SGK Toán 10 – Kết nối tri thức thuộc chương 4: Vectơ trong mặt phẳng. Bài tập này tập trung vào việc vận dụng các kiến thức về vectơ, đặc biệt là các phép toán cộng, trừ vectơ và tích của một số với vectơ để giải quyết các bài toán liên quan đến hình học.

Nội dung bài tập 5.24 trang 90 SGK Toán 10 – Kết nối tri thức

Bài tập yêu cầu học sinh chứng minh một đẳng thức vectơ liên quan đến trung điểm của các cạnh trong một hình bình hành. Cụ thể, cho hình bình hành ABCD, gọi I là trung điểm của cạnh AB, K là trung điểm của cạnh CD. Chứng minh rằng vectơ AI = vectơ CK.

Phương pháp giải bài tập 5.24 trang 90 SGK Toán 10 – Kết nối tri thức

Để giải bài tập này, chúng ta cần sử dụng các kiến thức sau:

Định nghĩa vectơ: Vectơ là một đoạn thẳng có hướng.
Phép cộng, trừ vectơ: Quy tắc hình bình hành, quy tắc tam giác.
Tích của một số với vectơ: Vectơ k.a cùng hướng với vectơ a nếu k > 0, ngược hướng nếu k < 0 và có độ dài bằng |k| lần độ dài của vectơ a.
Trung điểm của đoạn thẳng: Nếu M là trung điểm của đoạn thẳng AB thì vectơ AM = vectơ MB.

Lời giải chi tiết bài 5.24 trang 90 SGK Toán 10 – Kết nối tri thức

Gọi I là trung điểm của AB và K là trung điểm của CD. Ta cần chứng minh vectơ AI = vectơ CK.

Biểu diễn vectơ AI: Vì I là trung điểm của AB, ta có vectơ AI = 1/2 vectơ AB.
Biểu diễn vectơ CK: Vì K là trung điểm của CD, ta có vectơ CK = 1/2 vectơ CD.
Sử dụng tính chất của hình bình hành: Trong hình bình hành ABCD, ta có vectơ AB = vectơ DC. Do đó, vectơ CD = - vectơ AB.
Thay thế và kết luận: Từ các kết quả trên, ta có vectơ CK = 1/2 vectơ CD = 1/2 (- vectơ AB) = -1/2 vectơ AB. Tuy nhiên, điều này không đúng với yêu cầu chứng minh vectơ AI = vectơ CK. Cần xem lại đề bài hoặc cách tiếp cận. Đề bài có thể yêu cầu chứng minh vectơ AK = vectơ CI hoặc một đẳng thức khác.

(Lưu ý: Lời giải trên có thể cần điều chỉnh tùy thuộc vào cách diễn đạt chính xác của đề bài. Việc kiểm tra lại đề bài gốc là rất quan trọng.)

Ví dụ minh họa và bài tập tương tự

Để hiểu rõ hơn về cách giải các bài tập liên quan đến vectơ trong hình học, các em có thể tham khảo các ví dụ sau:

Bài tập 5.25 trang 90 SGK Toán 10 – Kết nối tri thức
Bài tập 5.26 trang 91 SGK Toán 10 – Kết nối tri thức

Lời khuyên khi học tập và giải bài tập về vectơ

Để học tốt môn Toán 10, đặc biệt là chương Vectơ, các em cần:

Nắm vững định nghĩa và các tính chất của vectơ.
Luyện tập thường xuyên các bài tập về phép cộng, trừ vectơ và tích của một số với vectơ.
Vận dụng kiến thức về vectơ để giải quyết các bài toán hình học.
Sử dụng hình vẽ để minh họa và hiểu rõ hơn về các bài toán.

Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ tự tin hơn trong việc giải bài tập 5.24 trang 90 SGK Toán 10 – Kết nối tri thức và các bài tập tương tự khác.